扩散模型与生成模型详解-慈云数据

扩散模型与其他生成模型

什么是扩散模型

扩散模型的简介

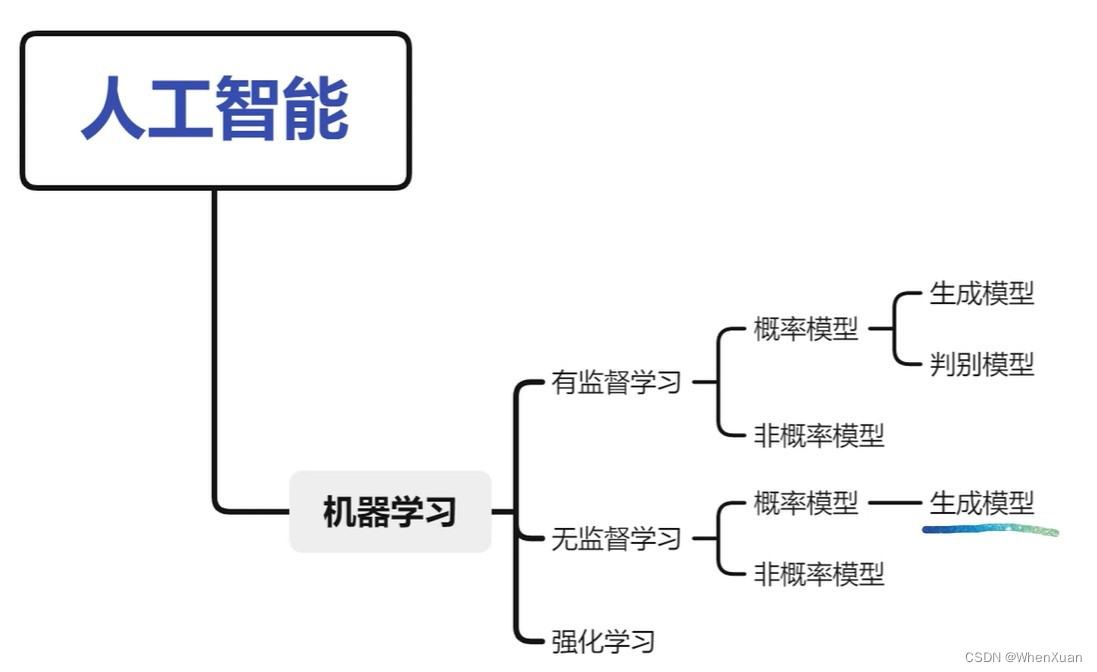
生成建模是理解自然数据分布的开创性任务之一。VAE、GAN和Flow系列模型因其实用性能而在过去几年中占据了该领域的主导地位。尽管取得了商业上的成功，但它们的理论和设计缺陷（棘手的似然计算、限制性架构、不稳定的训练动力学等）导致了一类名为“扩散概率模型”或DPM的新型生成模型的开发。

生成模型是一类可以根据某些隐含参数随机生成观察结果的模型。

近年来，扩散模型凭借其强大的生成能力成为一种新兴的生成模型。如今，已经取得了巨大的成就。

除了计算机视觉、语音生成、生物信息学和自然语言处理之外，该领域还有待探索更多的应用。

扩散模型的缺点

扩散模型有其真正的缺点：生成过程缓慢，数据类型单一，可能性低，无法降维。他们导致了许多改进的工作如下：

现针对扩散模型领域中存在的问题，提出了分类改进技术。
为了加速模型的改进，有一系列先进的技术来加速扩散模型——训练计划、无训练采样、混合建模以及评分和扩散统一。
对于数据结构多样化，我们提出了在连续空间、离散空间和约束空间中应用扩散模型的改进技术。
对于似然优化，我们提出了改进ELBO和最小化变分差的理论方法。
在降维方面，我们提出了几种解决高维问题的技术。
对于现有的模型，我们还根据具体的NFE提供了FID评分、IS和NLL的基准。
模型的简单原理与分类

扩散模型的目的是将先验数据分布转化为随机噪声，然后逐步修正变换，重建一个与先验分布相同的全新样本。

扩散模型的灵感来自非平衡热力学。他们定义了一个马尔可夫扩散步骤链，以缓慢地向数据添加随机噪声，然后学习逆转扩散过程以从噪声中构建所需的数据样本。与VAE或流动模型不同，扩散模型是通过固定程序学习的，并且潜在变量具有高维数（与原始数据相同）。

已经提出了几种基于扩散的生成模型，包括扩散概率模型（Sohl-Dickstein等人2015），噪声条件评分网络（NCSN;Yang & Ermon， 2019），以及去噪扩散概率模型（DDPM;何等人，2020年）。

分为正向过程（从 X0 到 XT）和反向过程（从 XT 到 X0）或者说是重建过程。

将起始状态转化为可处理噪声的过程是正向/扩散过程。

与正向过程相反方向的过程称为反向/去噪过程。

反向过程将噪声梯度逐步采样到样本中作为起始状态。

在任何一个进程中，任何两个状态之间的交换都是由转换内核实现的。

马尔科夫链

我们都知道无穷大样本下1-6每个数字出现的概率都是1/6，但想知道每一次掷色子的结果，我们永远无法准确计算预知，我们能想到的最好办法，就是用概论来描述这个结果。

随机过程

犹如牛顿定律在力学中所扮演的进行力学分析的角色，随机过程就是在概率论中，对事物变化研究运动的方法，对不确定性下的运动进行准确的数学描述。如同力学中对速度，加速度等概念的数学定义，随机过程中也定义了两个最重要的概念：概率空间、随机变量，在此不深入聊。

牛顿力学中，是确定性过程研究一个量随时间确定的变化，而随机过程描述的是一个量随时间可能的变化。在这个过程里，每一个时刻变化的方向都是不确定的，随机过程就是由这一系列不确定的随机变量组成的。每一个时刻系统的状态都由一个随机变量表述，整个过程则构成一个随机过程的实现。

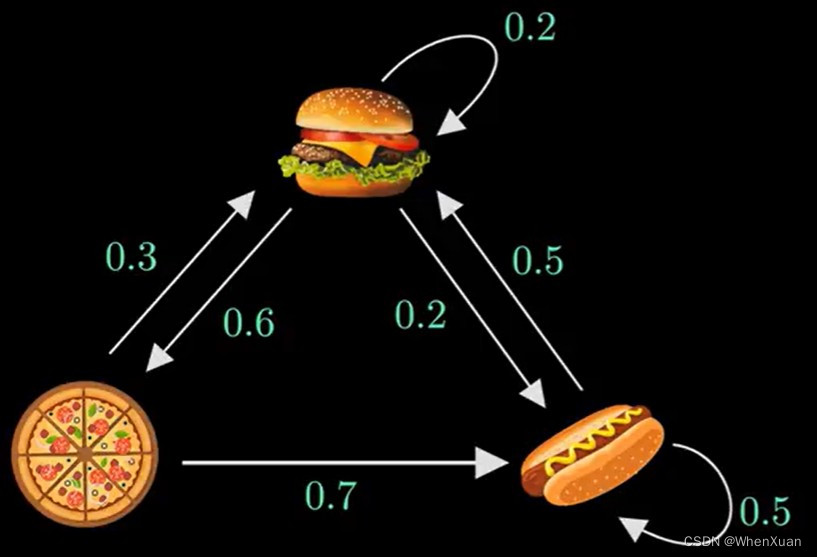
马尔科夫链的定义

知道了什么是随机过程后，我们可以试想一个最简单的随机过程，这个过程由N步组成，每一步都有两个选择（0，1），那么可能的路径就有2的N次方个，这个随机过程就要由2^N这个指数级别个数的概率来描述，我们一看指数级别！维度这么大岂不直接爆炸？？？

此刻，**马尔科夫过程(Markov Processes)**被推了出来：随机过程的每一步的结果与且仅与上一步有关，与其它无关。

makov过程用数学语言表述就是马尔可夫链(Markov chain)。马尔科夫链条中，随机过程的变化只取决于当下的变化而非历史，这种性质使得巨大的计算瞬时简化。

一个马尔科夫链实例

假设某人每天有三个状态：玩耍，学习，睡觉（这就是状态分布）。已知他今天在玩儿，那他明天学习、玩耍、睡觉的概率是多少？后天乃至N天后学习、玩耍、睡觉的概率是多少？

当然，想要知道N天后学习、玩耍、睡觉的概率是多少，我们需要有两个条件：
- 一个预知条件：知道他第一天的状态（状态分布矩阵或向量，用 S 表示），
- 一个假设：即他状态的转移都是有规律的，也就是今天学习，明天就玩儿或者睡觉或者还是继续学习的概率是确定的，简而言之，我们有预知确定的状态转移概率矩阵P。
  
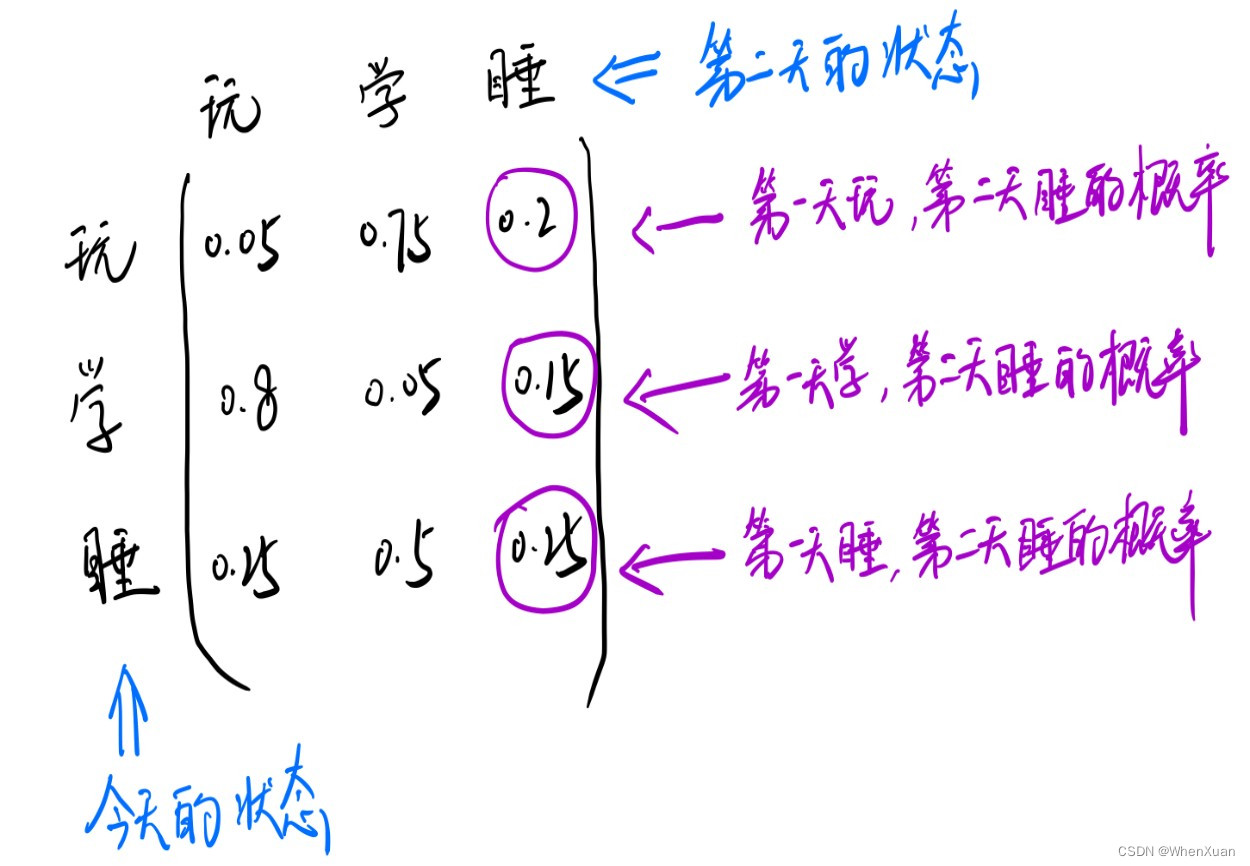
  上面这个矩阵就是确定的转移概率矩阵P，它具有时间齐次性，换句话说，也就是转移概率矩阵P它是保持不变的，第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。
  
  有了这个转移概率矩阵P，再加上已知的第一天的状态分布矩阵（他第一天在玩 or 学 or 睡的概率），就可以计算出进进第N天的状态分布了（他第N天在玩 or 学 or 睡的概率）。
  
  现在已经拥有了测算他 n 天后，是在玩还是在学，还是在睡的所有条件了，也就是初始状态分布矩阵S和转移概率矩阵P。
  
  假设他第一天的状态分布矩阵 S1 = [0.3, 0.4, 0.3]，里面的数字分别代表第一天这天在玩的概率，学的概率，和睡的概率。
  
  那么
  
  第二天玩学睡的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。
  
  第三天玩学睡的状态分布矩阵 S3 = S2 * P (只和S2有关)。
  
  第四天玩学睡的状态分布矩阵 S4 = S3 * P (只和S3有关)。
  
  …
  
  第n天玩学睡的状态分布矩阵 Sn = Sn-1 * P (只和Sn-1有关)。
  
  可以看到：马尔可夫链就是这样一个任性的过程，**它将来的状态分布只取决于现在，跟过去无关！**这就是马尔科夫过程(Markov Processes)的体现，他每天的可能的状态集合就构成了马尔可夫链(Markov chain)。
  
  因此马尔科夫链过程就是一个不断迭代的过程，可以通过循环来实现，记录每一步基于前一步的条件概率即可，由此最终通过连乘的方式完成最终的计算过程。
  
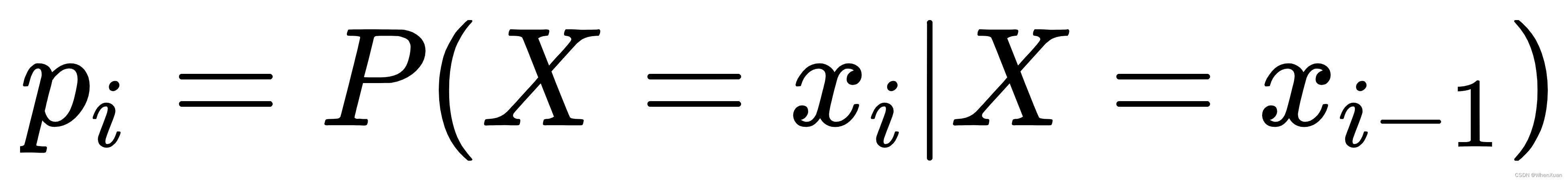
  代码实现
  
  Python 代码：
```
import numpy as np
matrix = np.matrix([[0.05, 0.75, 0.2],
                    [0.8, 0.05, 0.15],
                    [0.25, 0.5, 0.25]])
vector1 = np.matrix([[0.2, 0.6, 0.2]])
for i in range(100):
    vector1 = vector1 * matrix
    print('第{}轮'.format(i+1))
    print(vector1)
```
  运行结果：
```
...
第96轮
[[0.39781591 0.41341654 0.18876755]]
第97轮
[[0.39781591 0.41341654 0.18876755]]
第98轮
[[0.39781591 0.41341654 0.18876755]]
第99轮
[[0.39781591 0.41341654 0.18876755]]
第100轮
[[0.39781591 0.41341654 0.18876755]]
```
  从结果可以发现，已知一天初始状态和转移矩阵往后测算，当测算到某一天开始，往后的状态概率分布就不变了，一直保持[0.39781591, 0.41341654, 0.18876755]。这会不会是巧合？
  
  马尔科夫链的性质
  
  收敛性：
  
  由上面推到可以得到一个非常重要的性质：马尔可夫链模型的状态转移矩阵收敛到的稳定概率分布与初始状态概率分布无关。
  
  也就是说，在上面的那个例子中的初试状态矩阵，可以用任意的概率分布样本开始，只要马尔可夫链模型的状态转移矩阵确知，在一定规模的转换之后，我们就可以得到符合对应稳定概率分布的样本。
  
  最终达到的状态成为平稳状态 (equilibrum state) 或平稳分布 (stationary distribution)，表示这个链的概率分布不会再随时间而改变，可以说该马尔科夫链达到了收敛。
  
  常返性，不可约性：
  
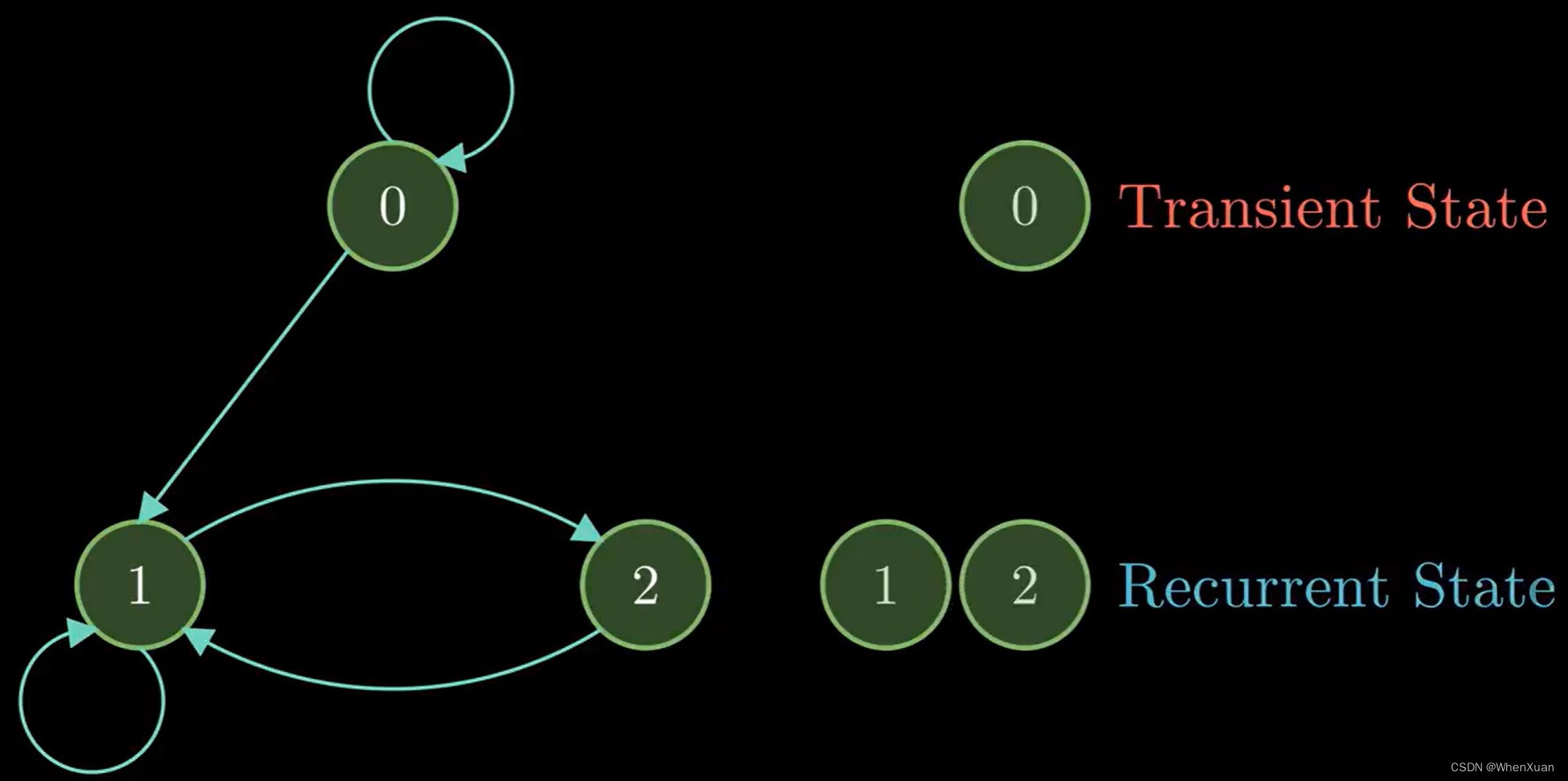
  有的马尔科夫过程中，某些状态只可能出现有限次（图中的0），称为暂态或非常返性。
  
  在无限次迭代中都可能会出现的状态称为常返态（图中的1和2）。
  
  当链中的某些状态不能到达时，称链的标记是可约的（reducible），本意是不可能在把这条链分解成可约的马尔科夫链。
  
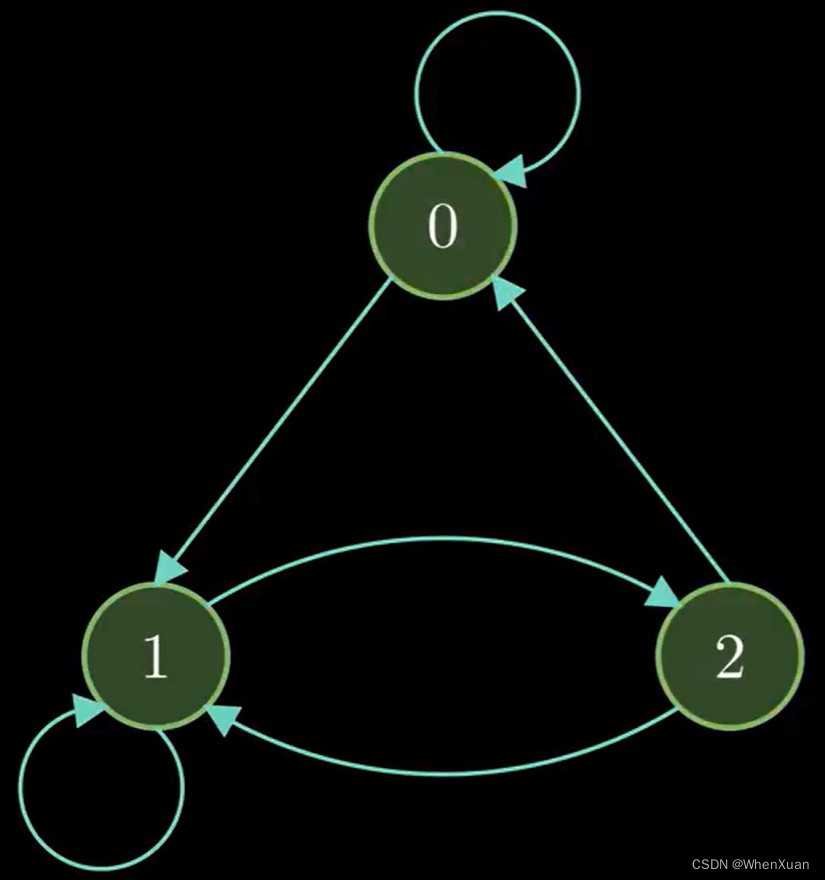
  当添加了到0点的边时，该图的任何顶点都是可达的，称为不可约链。
  
  扩散模型的工作方式
  
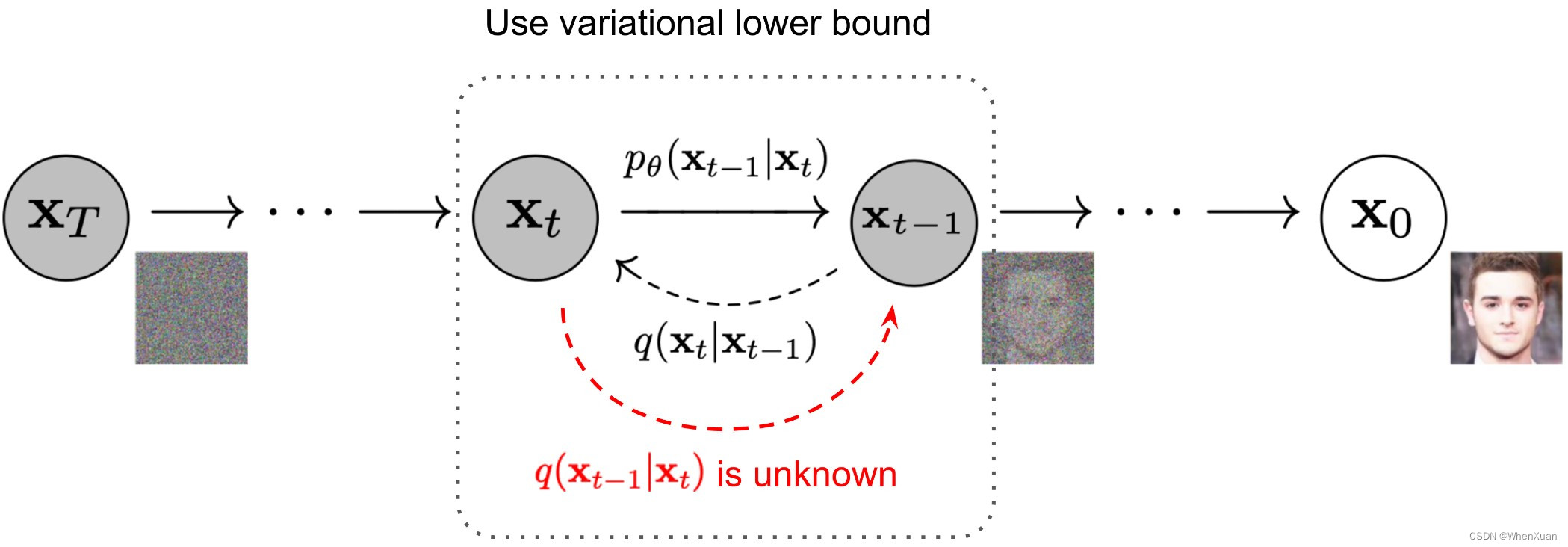
  生成模型：理解为扩散模型的逆过程从 XT 到 X0 的过程，是一个熵减小的过程，由原本的模糊分布生成我们想要的分布。
  
  扩散可以理解为一个水滴滴到河流中，就会慢慢的融入到河流中，逐步摆脱自己原本的分布，融入到新的分布中，是一个熵增的过程，从有序到无限的过程。
  
  逐步加一个噪声，最后会变成一个各项独立的高斯分布。
  
  扩散模型真正要做的事：我们有一堆 X0 的数据（这个人的照片），然后将 XT 到 X0 的逆扩散过程搞出来（原理或公式），这样我们就能随机的去生成一个噪声分布，然后利用这个噪声分布生成我们需要的数据（这个人的新照片）。
  
  对于图像主要包括两个过程：
  1. 固定（或预定义）的前向扩散过程 q 我们选择的，逐渐将高斯噪声添加到图像中，直到您最终得到纯噪声。
  2. 一种学习的反向去噪扩散过程pθ，其中神经网络被训练为从纯噪声开始逐渐对图像进行去噪，直到最终得到实际图像。
  正向和反向过程的索引由 t 发生在一定数量的有限时间步长中 T（DDPM 作者使用T=1000T=1 0 0 0)。你从t=0 对真实图像进行采样的位置x0从您的数据分布中，前向过程在每个时间步从高斯分布中采样一些噪声 t，将添加到上一个时间步长的图像中。给定足够大 T 以及在每个时间步添加噪声的良好时间表，您最终会得到所谓的各向同性高斯分布 t=T ，通过一个渐进的过程。
  
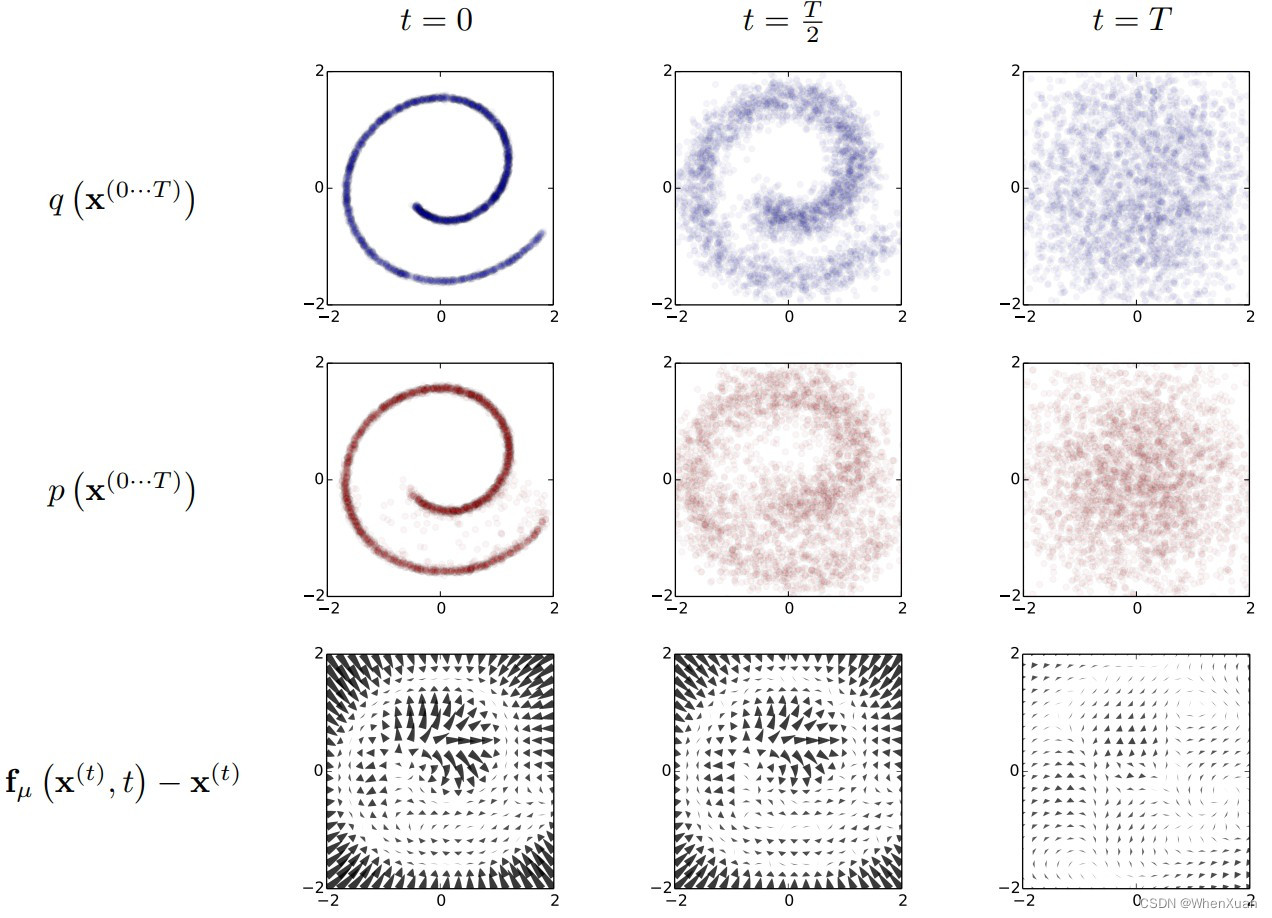
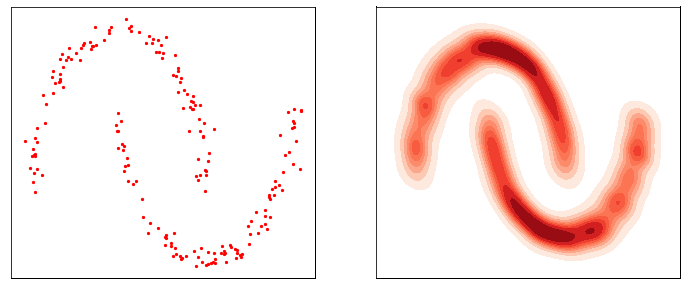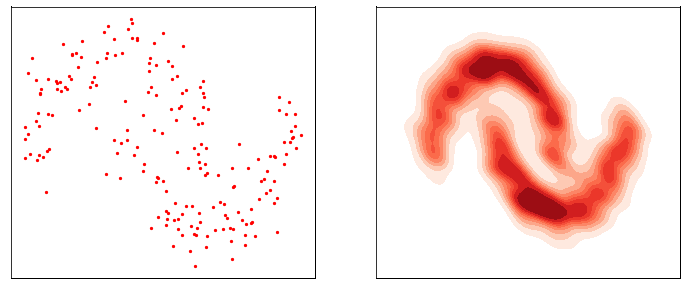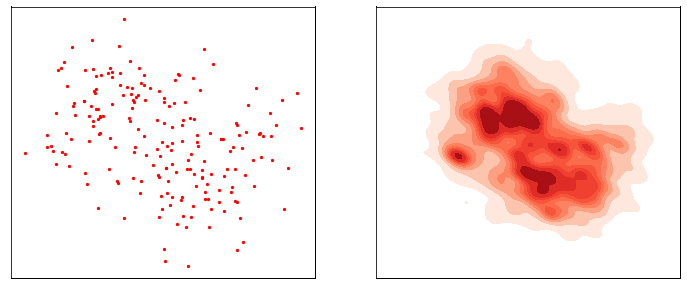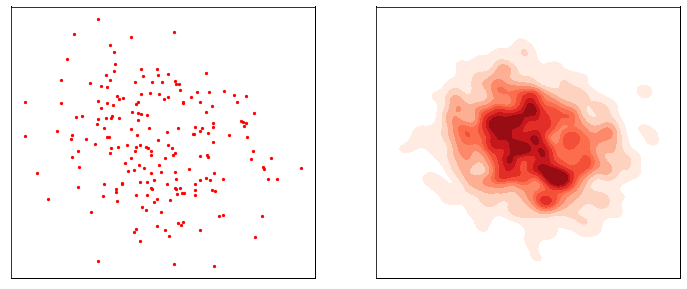
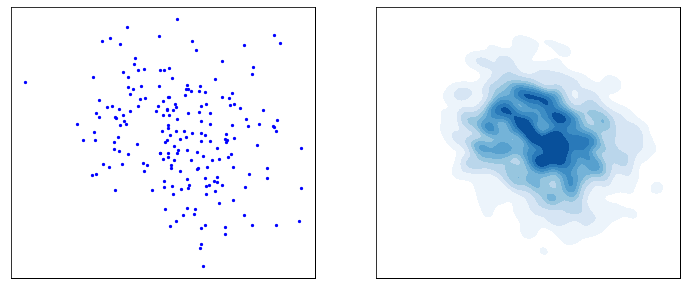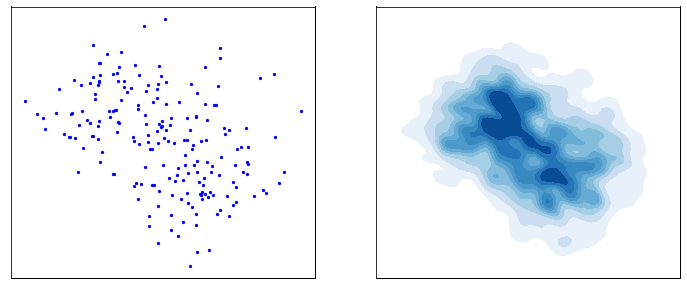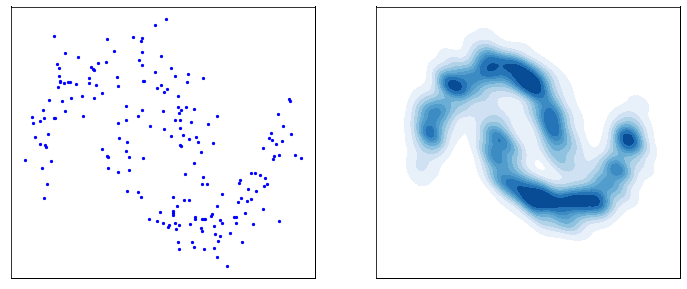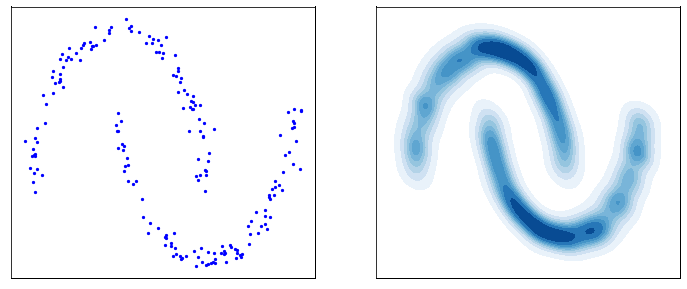
  **第一行图：**由原本的分布数据去获得一个高斯分布的过程，在这个过程中主要学习生成的步骤。
  
  **第二行图：**由随机生成的高斯分布获得新的原本分布的过程，是上一过程的一个逆过程。
  
  这两部都需要大量次数的迭代才能完成。
  
  第三行图：计算这个过程产生的差异叫做漂移差。
  
  正向扩散过程 Forward diffusion process
  1. 给定初始数据分布 X0 ~ q(x)，可以不断的向分布中添加高斯噪声，该噪声的标准差是以固定值 β 而确定的，均值是以固定值 β 和当前 t 时刻的数据 Xt 决定的，这个过程是一个马尔科夫链过程。
    
    正向过程是完全不含参数的，需要的参数都是已知的。
    
    我们每次加噪的高斯分布只与当前时刻的 Xt 和一个确定值 β 有关，不含可训练参数的。
    
    正向过程就是按照这种方式不断去迭代。
    
    β 在这里是一个0~1的小数但是会逐渐增长（和学习率逐渐降低相反）
  1. 随着 t 的不断增大，最终数据分布 XT 变成了一个各向独立的高斯分布。
  1. 任意时刻的 q(Xt) 的推到也可以完全基于 X0 和β来计算，而不需要做迭代，可以一步到位完成计算。
    
    重整化技巧：将 Xt 写成 Xt-1 和一个随机生成的正态分布的随机量。
    
    再将 Xt-1 重整化为 Xt-2。
  逆扩散过程 Reverse diffusion Process
  
  逆过程是从高斯噪声中恢复原始数据，我们可以假设它也是一个高斯分布，但是无法逐步地去拟合分布，所以需要构建一个参数分布来去做估计。逆过程仍然是一个马尔科夫链过程。
  
  这里假设一个含参的条件概论符合正态分布，输入也是 Xt 和 t 有关，最后写成一系列生产链的形式。
  
  对扩散模型的深入探索
  
  加速扩散模型采样
  
  通过遵循反向扩散过程的马尔可夫链从DDPM（去噪扩散概率模型）生成样品非常慢，因为T最多可以走一步或几千步。例如，从 DDPM 采样大小为 32 × 32 的 50k 图像大约需要 20 小时，但从 Nvidia 2080 Ti GPU 上的 GAN 采样不到一分钟。
  
  一种简单的方法是运行一个快速的采样计划，方法是每⌈T/S⌉减少过程的步骤T自S步骤。新的生成采样计划是{τ1，…，τS}哪里τ 1