
目录
1、归并排序
1.1、算法描述
1.2、图解说明
2、代码实现
3、master公式
3.1、公式以及结论
3.2、适用于某些特殊的递归
3.3、计算归并排序的时间复杂度

1、归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用递归或者说是分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
若将两个有序表合并成一个有序表,称为二路归并。
1.1、算法描述
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
而将两个的有序数列合并成一个有序数列,我们称之为"归并",这就是归并排序名字的由来。
1.2、图解说明
一句话简单说:对L到R范围排序,可以先求出L到R的中点M。先让左侧数据排好序,然后再让右侧数据排好序,此时再将两个有序子序列整合成一个新的有序序列。
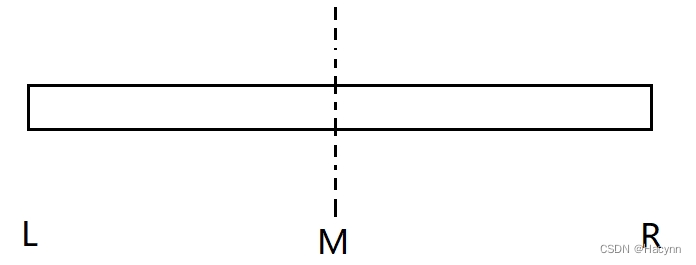
例如:
对一个数组[8,3,6,4,2,1,5,7]进行归并排序。
第一步:把长度为n的输入序列分成两个长度为n/2的子序列,新的子序列再分别分成两个长度为自身一半也就是n/4的子序列,以此类推。当分到单个子序列只剩下一个数字时,一个数字就是天然了有序,即此时左侧和右侧都排好序了。
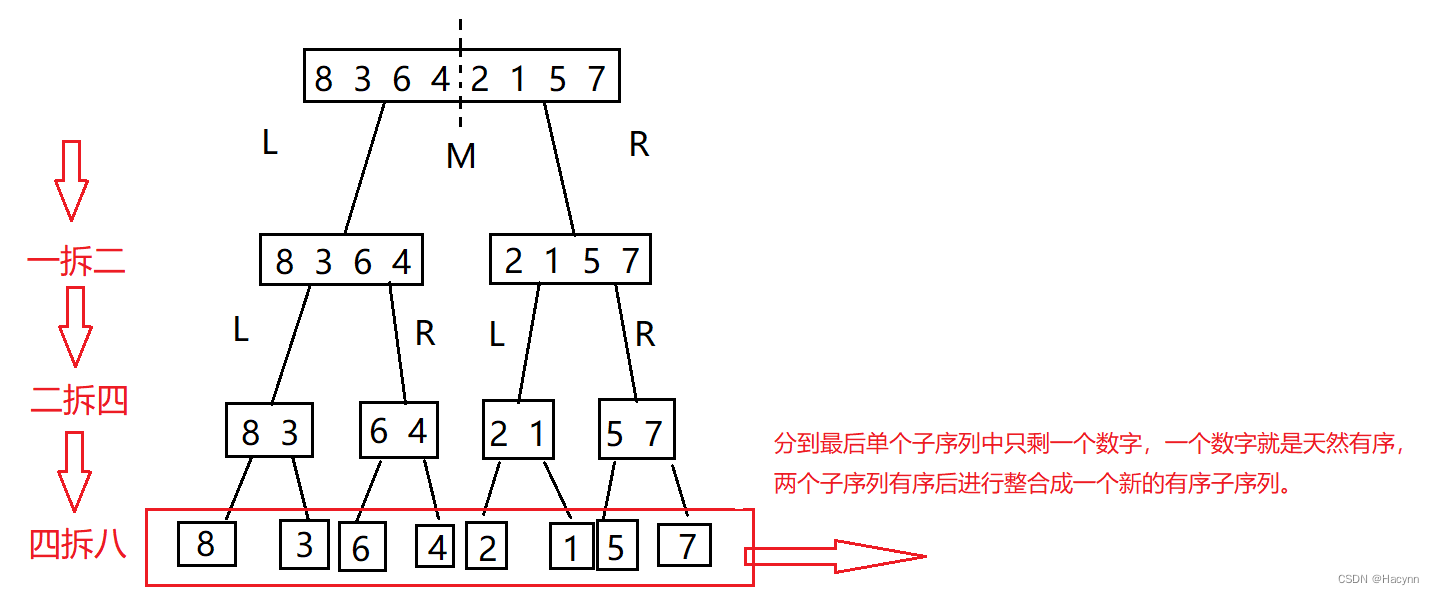
第二步:将两个排序好的子序列合并成一个新的排序序列。首先在每个子序列中都有一个指针指向子序列的第一个元素,两个指针的元素两两比较,较小的元素先放入新的子序列中,然后指针挪动继续比较,直至全部放入新的子序列当中,即完成一次子序列合并。慢慢合并最终使所有元素都成有序,即完成归并排序。

这个思路过程是非常精髓的,理解了这个思路之后,就可以试着用代码实现了。
2、代码实现
要使用归并,首先需要知道数组arr以及数组最左L下标和最右R下标,因此需要求出并带入MergeSort当中。
int main() { int arr[10] = { 8,3,6,4,2,1,5,7 }; int sz = sizeof(arr) / sizeof(arr[0]); MergeSort(arr, 0, sz - 1); int i = 0; for ( i = 0; i接下来看看MergeSort的实现。
- 首先是判断L是否等于R,如果L和R相等时就相当于是单个子序列中只存在了一个元素,而此时该子序列就为有序,因此不用进行操作直接返回即可,即if(L == R) return;
- 如果L不等于R时则认为该子序列中仍然可拆分,便求出mid中间值,并分别进行两次递归让两块递归范围有序,递归范围是L到mid、mid+1到R。
- 最后当递归结束时则代表L到mid、mid+1到R序列已有序,整体还无序,此时需要使用ExternalSort外部排序将这两个子序列整合成一个新的有序序列。
void MergeSort(int* arr, int L, int R) { if (L == R) //子序列只有一个数,默认为有序 { return; } int mid = L + (R - L) / 2; MergeSort(arr, L, mid); MergeSort(arr, mid + 1, R); ExternalSort(arr, L, mid, R); }ExternalSort的作用就是让arr中的L到M、M+1到R合并成一个新的有序序列,并将判断后的结果序列先存入到help指针指向的区域,等待完成所有合并,再将help整个区域的数据拷贝到arr对应的位置。
而存入help的规则是:
1、如果p1和p2都没有越界进行while循环:
p1和p2比较,如果p1大于p2,则将p2所指向的元素放入help中,然后将p2右移指向下一个,继续下一轮比较。
p1和p2比较,如果p1小于等于p2,则将p1所指向的元素放入help中,然后将p1右移指向下一个,继续下一轮比较。
2、如果有一方越界了,则退出循环,并判断p1和p2中哪个还有剩余的元素未排入help中,如果有则直接排入到help中。

void ExternalSort(int* arr, int L, int M, int R) { int* help = (int*)malloc(sizeof(int) * (R - L + 1)); //辅助空间,用于存放排序后的数据,空间大小为R-L+1。 if (help == NULL) { perror("ExternalSort->malloc"); return; } int helpSz = R - L + 1; int i = 0; int p1 = L; int p2 = M + 1; while (p1









