热门搜索
首页 技术支持 正文

【C++】哈希表

慈云数据 8个月前 (03-12) 技术支持 103 0

哈希表

  • 1.unorderd系列关联式容器
    • 1.1unordered_map+unordered_set介绍
    • 2.哈希表
      • 2.1闭散列 -- 开放地址法
        • 2.1.1线性探测
          • 插入
          • 查找
          • 删除
          • 针对插入查找做的修改
          • 线性探测完整代码
          • 2.1.2二次探测
          • 2.2开散列 -- 拉链法(哈希桶)
            • 插入
            • 查找
            • 删除
            • 除留余数法取质数
            • 拷贝构造
            • 赋值重载
            • 哈希桶完整代码

              在这里插入图片描述

              喜欢的点赞，收藏，关注一下把！在这里插入图片描述

              1.unorderd系列关联式容器

              在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到 l o g 2 N log_2 N log2​N，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想。最好的查询是，进行很少的比较次数就能够将元素找到，因此在C++11中，STL又提供了4个unordered系列的关联式容器，这四个容器与红黑树结构的关联式容器使用方式基本类似，只是其底层结构不同，本文中只对unordered_map和unordered_set进行介绍。

              1.1unordered_map+unordered_set介绍

              unordered_map在线文档说明

              unordered_set在线文档说明

              从功能上来说unordered_map和unordered_set和map和set基本上是一样的，只不过unorder_map和unordered_set底层是哈希表。map和set底层是搜索树，所以迭代器在走的时候map和set是有序的，unordered_map和unordered_set是无序的。

              因为底层不同，所以给它们一个Hash的仿函数，这个是什么我们学了底层就知道了。

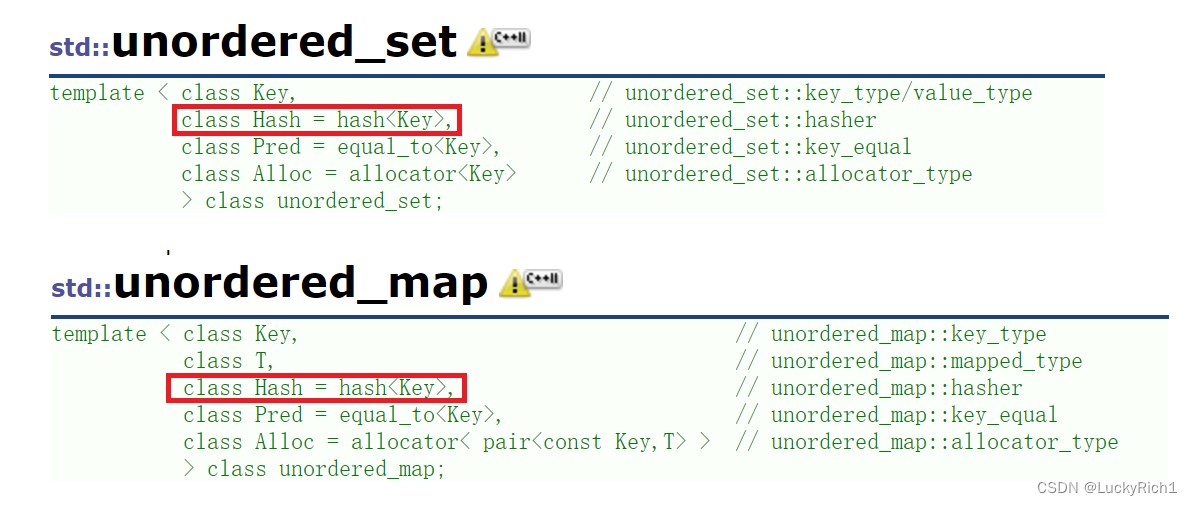
              在这里插入图片描述

              并且还是因为底层不同，它们只有单向迭代器。只支持++，不支持- -

              在这里插入图片描述

              哈希表有多种实现方式，库选择桶的实现方式封装unordered_map和unordered_set，因此它们的底层也可以叫做哈希桶。

              下面是对桶操作，不过这些接口我们平常很少用，了解即可。

              在这里插入图片描述

              size_t bucket_count()const返回哈希桶中桶的总个数
              size_t bucket_size(size_t n)const返回n号桶中有效元素的总个数
              size_t bucket(const K& key)返回元素key所在的桶号

              这是有关负载因子的操作，也不用管。

              在这里插入图片描述

              这些东西等我们学过它们的底层之后我们就懂了。

              剩下的接口就和map和set几乎差不多，这样的好处也是减轻我们的学习成本。既然unordered_map，unordered_set和map，set接口这么相似，那封装出它们有什么用呢，我们从各自的效率对比来看一看。

              以unordered_set和set对比为例，注意对比性能走Release

              插入

              int main()
{
	size_t N = 1000000;
	unordered_set us;
	set s;
	vector v;
	v.reserve(N);
	srand((unsigned int)time(nullptr));
	for (size_t i = 0; i  

              插入完整代码
               

              bool Insert(const pair& kv)
{
	//防止插入相同的值
	if (Find(kv.first))
		return false;
	//负载因子控制在1,超过就扩容
	if (_n == _tables.size())
	{
		vector newtable;
		newtable.resize(_tables.size() * 2);
		for (size_t i = 0; i _next;
				size_t hashi = Hash()(cur->_kv.first) % newtable.size();
				cur->_next = newtable[hashi];
				newtable[hashi] = cur;
				cur = next;
			}
			_tables[i] = nullptr;
		}
		_tables.swap(newtable);//旧表和新表交换一下
	}
	//匿名对象去调用仿函数,算在第几个桶里面
	int hashi = Hash()(kv.first) % _tables.size();
	//头插
	Node* newnode = new Node(kv);//调用Node的构造,因此Node写个构造
	newnode->_next = _tables[hashi];
	_tables[hashi] = newnode;
	++_n;
	return true;
}

               

              删除
               

              删除不能再直接查找了，然后就删除了。因为我们这是单链表，需要知道该节点前一个位置！也不能使用单链表那种O(1)那种覆盖删除法。
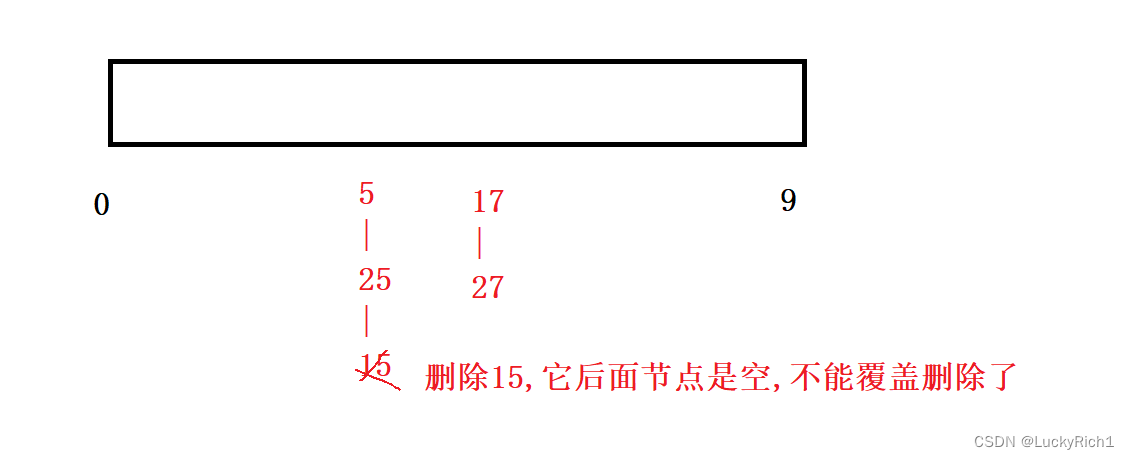
              在这里插入图片描述
              所以老老实实的去找，然后再删。
               

              bool Erase(const K& key)
{
	size_t hashi = Hash()(key) % _tables.size();
	Node* cur = _tables[hashi];
	Node* prev = nullptr;//记录被删节点前一个位置
	while (cur)
	{
		if (cur->_kv.first == key)
		{
			if (cur == _tables[hashi])//被删节点是头一个节点
			{
				_tables[hashi] = cur->_next;
			}
			else 
			{
				prev->_next = cur->_next;
			}
			delete cur;
			return true;
		}
		else
		{
			prev = cur;
			cur = cur->_next;
		}
	}
	return false;
}

               

              除留余数法取质数
               

              这里我们看看库是怎么取的
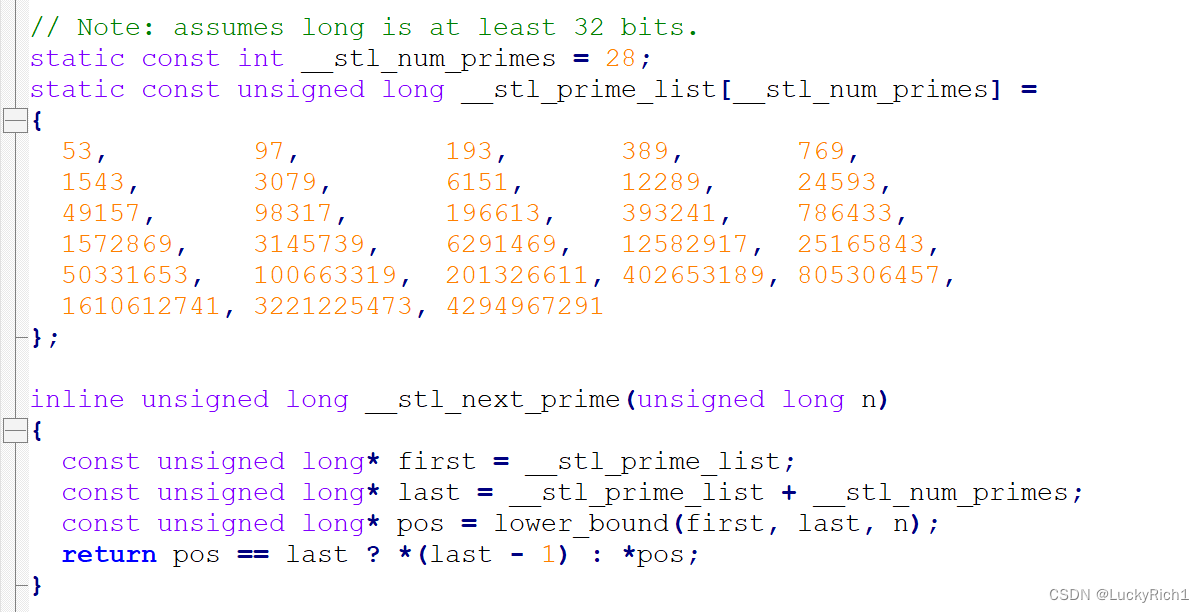
              在这里插入图片描述
              库里给我们定义了一个质数表，第一次是53扩容2倍是106肯定不是质数了，因此选了一个靠近106的质数97，也算是接近2倍空间扩容了。
               

              在我们的代码哈希表也加上这个取质数的函数。
               

              inline unsigned long __stl_next_prime(unsigned long n)
{
	static const int __stl_num_primes = 28;
	static const unsigned long __stl_prime_list[__stl_num_primes] =
	{
	  53,         97,         193,       389,       769,
	  1543,       3079,       6151,      12289,     24593,
	  49157,      98317,      196613,    393241,    786433,
	  1572869,    3145739,    6291469,   12582917,  25165843,
	  50331653,   100663319,  201326611, 402653189, 805306457,
	  1610612741, 3221225473, 4294967291
	};//最大质数取得是靠近整型最大数得质数
	for (size_t i = 0; i  n)
			return __stl_prime_list[i];
	}
	//不用担心会哈希表会扩到最大质数,因为这时对于整型来说都已经差不多48G了
	return __stl_prime_list[__stl_num_primes - 1];
}

               

              构造和插入扩容也都需要改一下
              构造获取比0大的质数
              插入扩容获取比当前空间大的质数
              在这里插入图片描述
               

              拷贝构造
               

              HashTable(const HashTable& ht)
	:_n(ht._n)
{
	_tables.resize(ht._tables.size());
	for (size_t i = 0; i _kv);
			_tables[i] = copy;
			//如果该链表不止一个节点，把其他节点拿下来重新申请节点尾插
			while (cur->_next)
			{
				cur = cur->_next;
				//尾插
				copy->_next = new Node(cur->_kv);
				copy = copy->_next;
			}
		}
	}
}

               

              赋值重载
               

              //赋值重载现代写法 复用拷贝构造
HashTable& operator=(HashTable ht)
{
	_n = ht._n;
	_tables.swap(ht._tables);
	return *this;//返回之前会自动调用HashTable的析构，释放对象ht
}

               

              哈希桶完整代码
               

              	template
	struct HashFunc
	{
		//凡是能转成整型的就转成整型 如负数,如指针,如浮点数
		//string不能转
		size_t operator()(const K& key)
		{
			return (size_t)key;
		}
	};
	//模板特化
	template
	struct HashFunc
	{
		//BKDR
		size_t operator()(const string& key)
		{
			size_t num = 0;
			for (auto& ch : key)
			{
				num *= 131;
				num += ch;
			}
			return num;
		}
	};
	template
	struct HashNode
	{
		pair _kv;
		HashNode* _next;
		HashNode(const pair& kv)
			:_kv(kv)
			,_next(nullptr)
		{}
	};
	template
	class HashTable
	{
		typedef HashNode Node;
	public:
		HashTable()
			:_n(0)//这里虽然没有明确写调用vector构造,但是编译器会按照声明顺序去调用的,所以会自动调用vecto的构造
		{
			//_tables.resize(10);//调用HashNode的构造
			_tables.resize(__stl_next_prime(0));
		}
		~HashTable()
		{
			for (size_t i=0;i
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur-_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}//走到这里会自动调用vector的析构
		HashTable(const HashTable& ht)
			:_n(ht._n)
		{
			_tables.resize(ht._tables.size());
			for (size_t i = 0; i _kv);
					_tables[i] = copy;
					while (cur->_next)
					{
						cur = cur->_next;
						//尾插
						copy->_next = new Node(cur->_kv);
						copy = copy->_next;
					}
				}
			}
		}
		//赋值重载现代写法 复用拷贝构造
		HashTable& operator=(HashTable ht)
		{
			_n = ht._n;
			_tables.swap(ht._tables);
			return *this;
		}
		bool Insert(const pair& kv)
		{
			if (Find(kv.first))
				return false;
			//负载因子控制在1,超过就扩容
			if (_n == _tables.size())
			{
				vector newtable;
				//newtable.resize(_tables.size() * 2);
				newtable.resize(__stl_next_prime(_tables.size()));
				for (size_t i = 0; i _next;
						size_t hashi = Hash()(cur->_kv.first) % newtable.size();
						cur->_next = newtable[hashi];
						newtable[hashi] = cur;
						cur = next;
					}
					_tables[i] = nullptr;
				}
				_tables.swap(newtable);//旧表和新表交换一下
			}
			//匿名对象去调用仿函数,算在第几个桶里面
			int hashi = Hash()(kv.first) % _tables.size();
			//头插
			Node* newnode = new Node(kv);//调用Node的构造,因此Node写个构造
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;
			return true;
		}
		Node* Find(const K& key)
		{
			size_t hashi = Hash()(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
					return cur;
				else
					cur = cur->_next;
			}
			return nullptr;
		}
		bool Erase(const K& key)
		{
			size_t hashi = Hash()(key) % _tables.size();
			Node* cur = _tables[hashi];
			Node* prev = nullptr;//记录被删节点前一个位置
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					if (cur == _tables[hashi])//被删节点是头一个节点
					{
						_tables[hashi] = cur->_next;
					}
					else 
					{
						prev->_next = cur->_next;
					}
					delete cur;
					return true;
				}
				else
				{
					prev = cur;
					cur = cur->_next;
				}
			}
			return false;
		}
		inline unsigned long __stl_next_prime(unsigned long n)
		{
			static const int __stl_num_primes = 28;
			static const unsigned long __stl_prime_list[__stl_num_primes] =
			{
			  53,         97,         193,       389,       769,
			  1543,       3079,       6151,      12289,     24593,
			  49157,      98317,      196613,    393241,    786433,
			  1572869,    3145739,    6291469,   12582917,  25165843,
			  50331653,   100663319,  201326611, 402653189, 805306457,
			  1610612741, 3221225473, 4294967291
			};//最大质数取得是靠近整型最大数得质数
			for (size_t i = 0; i  n)
					return __stl_prime_list[i];
			}
			//不用担心会哈希表会扩到最大质数,因为这时对于整型来说都已经差不多48G了
			return __stl_prime_list[__stl_num_primes - 1];
		}
	private:
		vector _tables;
		size_t _n;
	};
海报

猜你喜欢

php redis分布式锁

php redis分布式锁
linux内存缓存占用过高分析和优化

linux内存缓存占用过高分析和优化
stm32编写Modbus步骤

stm32编写Modbus步骤
如何保证数据库和缓存的一致性

如何保证数据库和缓存的一致性
Mongodb聚合操作中的$unset

Mongodb聚合操作中的$unset
私域引流宝PHP源码 以及搭建教程

私域引流宝PHP源码 以及搭建教程
400-801-9632
微信扫一扫加客服

微信扫一扫加客服

851239876
点击启动AI问答
Draggable Icon