标题~
- 本系列文章主要用于笔者期末复习,行文混乱,请见谅
- 备考补充及零碎知识点
- 弱对偶定理
- 推论
- 最优性
- 强对偶定理
- 互补松弛性✨
- 证明过程(推荐看一看)
- 换言之:对偶变量和松弛变量的乘积为0
- 例子
- 应用
- 影子价格
- 定义
- 内涵
- 注意
- 问题
- 检验数的意义
- 问题
- 问题:什么是退化的最优解
- 对偶问题的引入
- 从另一个角度思考
- 总结
- 对偶问题的一般形式
- 原问题
- 对偶问题
- ✨以矩阵描述(更加直观)
- 多做题,就知道什么是对偶了
- 对称形式
- 非对称形式✨✨✨【一定要掌握】
- 规律
- 推导过程
- 复习单纯形法计算过程
- 举例说明
- 对偶单纯形法
- 单纯形法基本思路
- ❓问题:怎么(什么时候)添加人工变量
- ❓问题:有非零人工变量怎么办
- 对偶单纯形法基本思路
- 确定初始基解
- 问题 为什么对偶问题的最优性一直都是满足的
- 跟单纯形法的区别与联系✨✨
- 例题讲解✨✨🙌
- 注意看,对偶单纯形法的条件是min还是max【我看到的是min配合大于等于】
- 注意:对偶问题不需要用对偶表,看视频就好⚠️⚠️⚠️⚠️
- 下面的例题做法非考试正规做法!!但是求单纯形法规则是一样的
- 运输问题建模
- 产销平衡问题
- 建立模型
- 求解模型【表上作业法】
- 确定可行解方法①:左上角填充法
- 确定可行解方法②:最小元素法
- 确定可行解方法③:沃格尔法
- 迭代方法①:闭回路法
- 入基变量选择
- 出基变量选择
- 产销不平衡问题
- 产量大于销量
- 有转运的问题
- 产销不确定
听说运筹学这门课挺好的,有值得一听的必要;此篇用作课堂总结、期末复习及记录。
或许与教材内容会有很大程度重复。
本系列文章主要用于笔者期末复习,行文混乱,请见谅
本章开始会适当结合一些B站网课【运筹学】应试向基础教程
备考补充及零碎知识点
- 对偶问题的对偶问题就是原问题
- 矩阵表达
- 要弄清楚矩阵
A
A
A和
C
C
C分别是什么

- 最好记住这几个矩阵,进而记住弱对偶定理,松弛定理
弱对偶定理
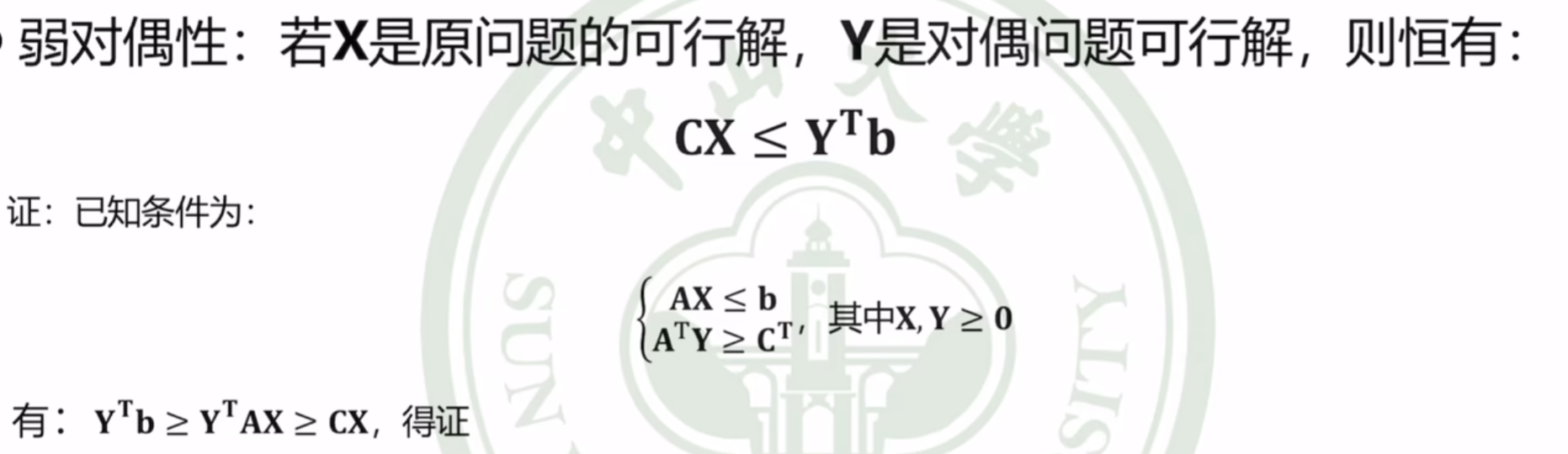
结合着矩阵形式表述
推论
- 原问题最优解目标函数值是对偶问题目标函数值的下界,对偶问题最优解目标函数值是原问题目标函数值的上界。
对偶问题的解一定大于原问题的解
- 原问题有无界解→对偶问题无可行解,对偶问题有无界解→原问题无可行解,但逆不成立(对偶问题无可行解时,原问题也可能无可行解)
- 原问题有可行解而对偶问题无可行解→原问题为无界解,反之(对调"原问题"和"对偶问题")亦然
最优性

强对偶定理

互补松弛性✨
互补松弛性😦双最优解情况下)若原问题中某一约束条件对应的对偶变量( y i y_i yi)值为非零,则该约束条件取严格等式;若约束条件取严格不等式,则其对应的对偶变量一定为0,即:
- 若 y i > 0 y_{i}>\mathbf{0} yi>0 ,则有 ∑ j = 1 n a i j x j = b i \sum_{j=1}^{n} a_{i j} x_{j}=b_{i} ∑j=1naijxj=bi , 即松弛变量值为 0
- 若 ∑ j = 1 n a i j x j
- 原问题最优解目标函数值是对偶问题目标函数值的下界,对偶问题最优解目标函数值是原问题目标函数值的上界。









