目标检测--边框回归损失函数SIoU原理详解及代码实现

边框回归损失函数

• • 1. SIoU
  • • 1.1 原理
    • 1.2 代码实现

      1. SIoU

      1.1 原理

      有关IoU损失函数，如(GIoU, DIoU, CIoU)没有考虑到真实框与预测框框之间的方向，导致收敛速度较慢，对此SIoU引入真实框和预测框之间的向量角度，重新定义相关损失函数，具体包含四个部分：

      （1）角度损失(Angle cost)，定义如下

      

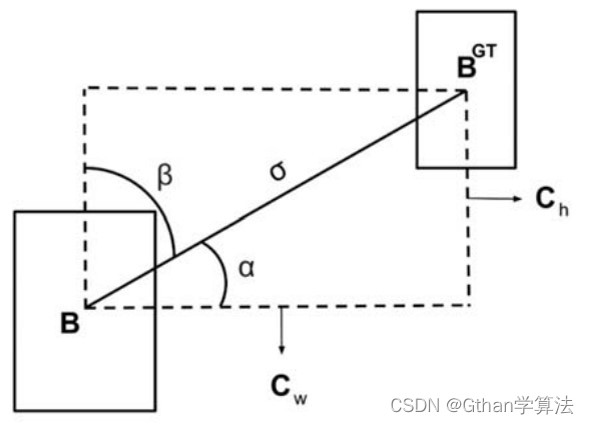
      Λ = 1 − 2 ∗ sin ⁡ 2 ( arcsin ⁡ ( c h σ ) − π 4 ) = cos ⁡ ( 2 ∗ ( arcsin ⁡ ( c h σ ) − π 4 ) ) \Lambda = 1-2*\sin^2(\arcsin(\frac{c_h}{\sigma}) - \frac{\pi}{4})=\cos(2*(\arcsin(\frac{c_h}{\sigma}) - \frac{\pi}{4})) Λ=1−2∗sin2(arcsin(σch​​)−4π​)=cos(2∗(arcsin(σch​​)−4π​))

      其中 c h c_h ch​为真实框和预测框中心点的高度差， σ \sigma σ为真实框和预测框中心点的距离，事实上 arcsin ⁡ ( c h σ ) \arcsin (\frac{c_h}{\sigma}) arcsin(σch​​)等于角度 α \alpha α

      c h σ = sin ⁡ ( α ) \frac{c_h}{\sigma}=\sin(\alpha) σch​​=sin(α)

      σ = ( b c x g t − b c x ) 2 + ( b c y g t − b c y ) 2 \sigma = \sqrt{(b_{c_x}^{gt}-b_{c_x})^2+(b_{c_y}^{gt}-b_{c_y})^2} σ=(bcx​gt​−bcx​​)2+(bcy​gt​−bcy​​)2 ​

      c h = max ⁡ ( b c y g t , b c y ) − min ⁡ ( b c y g t , b c y ) c_h = \max(b_{c_y}^{gt}, b_{c_y}) - \min(b_{c_y}^{gt}, b_{c_y}) ch​=max(bcy​gt​,bcy​​)−min(bcy​gt​,bcy​​)

      ( b c x g t , b c y g t ) (b_{c_x}^{gt}, b_{c_y}^{gt}) (bcx​gt​,bcy​gt​)为真实框中心坐标 ( b c x , b c y ) (b_{c_x}, b_{c_y}) (bcx​​,bcy​​)为预测框中心坐标，可以注意到当 α \alpha α为 π 2 \frac{\pi}{2} 2π​或0时，角度损失为0，在训练过程中若 α