经实验证明,采用混沌映射产生随机数的适应度函数值有明显提高,用混沌映射取代常规的均匀分布的随机数发生器可以得到更好的结果,特别是搜索空间中有许多局部解时,更容易搜索到全局最优解,利用混沌序列进行种群初始化、选择、交叉和变异等操作会影响算法的整个过程,而且常常能取得比伪随机数更好的效果。
混沌主要具有以下两个性质:
- 轨道不稳定性,这个性质在适当的约束条件下导致运动的不稳定性和分叉现象
- 高度依赖初始值,即两个相近的初始值会得到完全不相同的随机数序列
描述混沌运动的一个典型例子,就是非线性Logistic映射,它是一个一维的非线性函数:
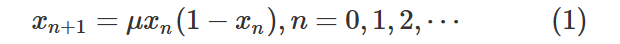
式中,μ为控制参数,且μ>1;xn的取值范围为0≤xn≤1。
本篇博客以logistic混沌映射为例来学习混沌映射的性质。
本文考虑控制参数μ在1
