黏菌算法（Slime Mould Algorithm，SMA）

文章目录

• 1 算法思想
• 2 算法步骤
• 3 求函数最值（Python实现）
• 4 算法进阶
• • 直接改进SMA
  • 融合别的智能优化算法来改进SMA
  • SMA及其改进的应用

    1 算法思想

    黏菌算法由李世民等人发表于2020年，模拟了黏菌觅食过程中的行为和形态变化。

    黏菌在有丝分裂后形成的变形体成熟之后，进入营养生长时期，会形成网状型态，且依照食物、水与氧气等所需养分改变其表面积。在黏菌算法中，黏菌会根据当前位置的客观条件（适应度函数优劣），决定每个个体所在位置的权重，然后个体会根据权重决定新的位置在哪。

    当黏菌接近食物源时，生物振荡器会通过静脉产生传播波，来增加细胞质流量。食物浓度越高，生物振荡器产生的传播波越强，细胞质流动越快。黏菌算法就是通过模拟黏菌这种捕食行为来实现智能寻优功能的。

    借鉴黏菌的生物行为，可以抽象出三个规则：

    1. 接近食物： 黏菌通过空气中的气味接近食物，黏菌接近食物时呈圆形与扇形结构运动。
    2. 包围食物： 黏菌静脉接触的食物浓度越高，生物振荡器产生的传播波越强，细胞质流动越快。
    3. 抓取食物： 黏菌在食物浓度低时更慢地接近食物，找到优质食物时更快地接近食物。

    2 算法步骤

    1. 设置参数，初始化种群，计算适应度值；
    2. 更新黏菌权重W、参数a、参数b：

       W = { 1 + r × l o g ( b F − S ( i ) b F − w F + 1 ) , i f 该 个 体 的 适 应 度 值 排 在 群 体 前 一 半 1 − r × l o g ( b F − S ( i ) b F − w F + 1 ) , e l s e 在 后 一 半 W=\left\{ \begin{aligned} 1+r×log(\frac{bF-S(i)}{bF-wF}+1) , & if 该个体的适应度值排在群体前一半 \\ 1-r×log(\frac{bF-S(i)}{bF-wF}+1) , & else 在后一半 \end{aligned} \right. W=⎩⎪⎪⎨⎪⎪⎧​1+r×log(bF−wFbF−S(i)​+1),1−r×log(bF−wFbF−S(i)​+1),​if该个体的适应度值排在群体前一半else在后一半​

       （下面有参数说明表）

       公式解读：前一半较优部分个体的权重取值较大，在[1,1.3]内；较差的后一半取值在[0.7,1]内，越差的个体权重越接近0.7。取log的作用就是减缓了W的变化率。

       a = a r c t a n h ( b ) b = 1 − t T a=arctanh(b) \\ b=1-\frac{t}{T} a=arctanh(b)b=1−Tt​

       b的变化是一条线性递减的简单直线，a的变化如下图：

       

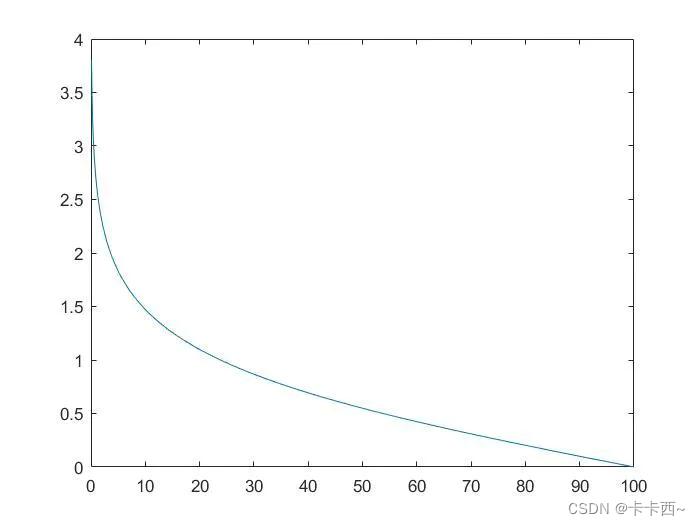
    3. 更新个体位置 X ( t + 1 ) X(t+1) X(t+1)，分三种情况：

       X ( t + 1 ) = { r × ( u b − l b ) + l b , r