提示：文章寫完後，目錄可以自## 标題動生成，如何生成可參考右邊的幫助文檔
文章目錄
- 一、A*算法的由來及應用背景
- 二、A*算法的基本原理
- 1.基本數學原理
- 2.啓發函數的選擇
- 2.1曼哈頓距離
- 2.2對角距離（切比雪夫距離）
- 2.3歐幾裏德距離
- 三、A*算法的程序實現
- 1.算法邏輯
- 2.實驗結果
- 四、A*算法的總結
- A*算法的優缺點
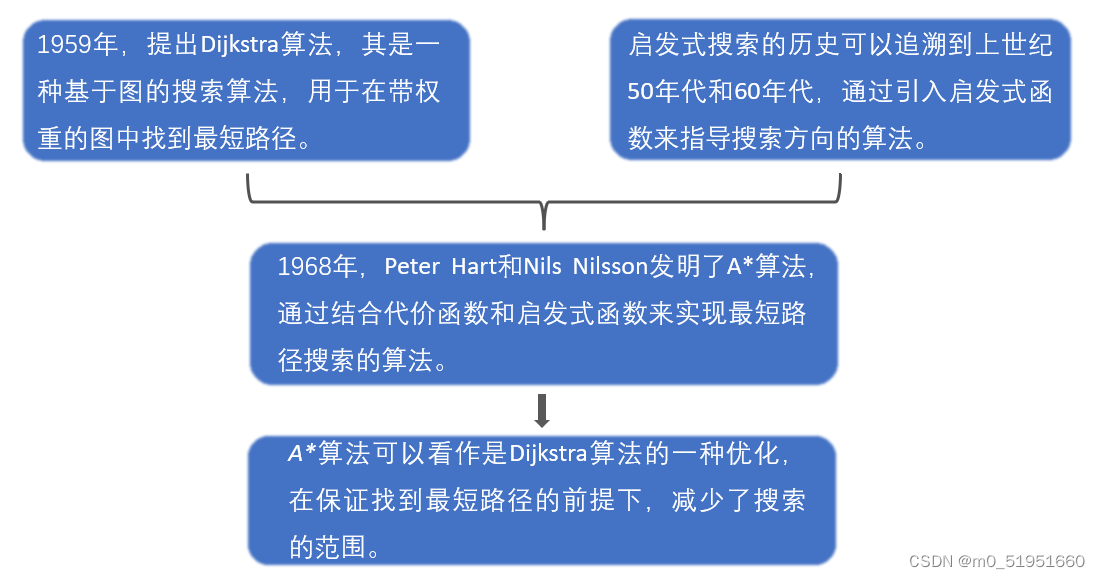
一、A*算法的由來及應用背景
二、A*算法的基本原理
1.基本數學原理
A*算法作爲啓發式搜索算法，其更新估值F來進行搜索
F = G + H F=G+H F=G+H
F F F: 當前節點的總代價
G G G: 開始節點到當前節點的移動距離（實際代價）
H H H: 從當前節點到終點的估計移動距離（估計代價）
計算G代價爲從起點到當前節點經過的所有邊的距離之和。
計算H代價的啓發函數h包括曼哈頓距離、對角距離（切比雪夫距離）、歐幾裏德距離。
注意點：
1.計算H時，要忽略路徑中的障礙物。這是對剩餘距離的估算值，而不是實際值，因此H代價爲估計代價。
2.在進行全局地圖路徑規劃時，将環境信息轉化爲一個網格地圖，其中每個網格表示環境的一個區域，障礙物的區域可以标記爲障礙物網格，因此障礙物節點是已知的。
3.已知A*算法保證能夠找到最短路徑的條件是滿足以下兩個條件：
（1）啓發函數h(n)必須滿足單調性（即估計的代價不會超過從節點n到目标節點的實際代價），
（2）地圖必須是可行的，即不存在無法通過的障礙物或無法到達的區域。
2.啓發函數的選擇
2.1曼哈頓距離
曼哈頓距離： D = ∣ x 2 − x 1 ∣ + ∣ y 2 − y 1 ∣ D=|x_{2}-x_{1}|+|y_{2}-y_{1}| D=∣x2−x1∣+∣y2−y1∣，如下圖：
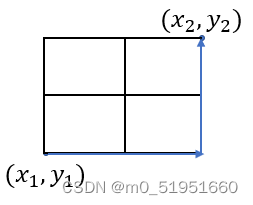
如果圖形中隻允許朝上下左右四個方向移動，則可以使用曼哈頓距離。計算從當前栅格橫向或縱向移動到達目标所經過的方格數。
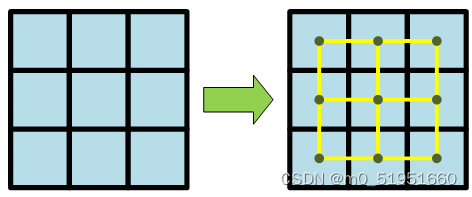
例如在上圖中中心節點可以朝着上下左右拓展，這時采用曼哈頓距離作爲啓發函數更有效。當拓展節點存在障礙物時：
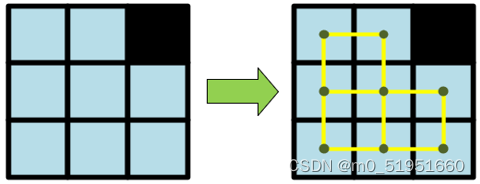
A*算法會根據地圖中的網格來判斷每個節點的狀态，即是否爲障礙物節點。當算法擴展節點時，如果該節點是障礙物節點，則不會将其加入到待擴展節點集合中，從而避免沿着該節點繼續搜索，這樣就能夠有效地避免穿越障礙物。
2.2對角距離（切比雪夫距離）
對角距離（切比雪夫距離）： D = m a x ( ∣ x 2 − x 1 ∣ + ∣ y 2 − y 1 ∣ ) D=max(|x_{2}-x_{1}|+|y_{2}-y_{1}|) D=max(∣x2−x1∣+∣y2−y1∣),如下圖：
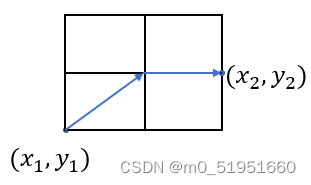
如果圖形中允許朝八個方向移動，則可以使用對角距離。對角距離更适合處理允許斜向移動的情況，因爲它考慮了斜向移動時的額外距離，使得估算更加準确。
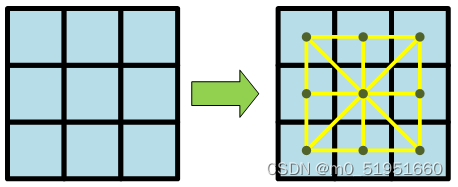
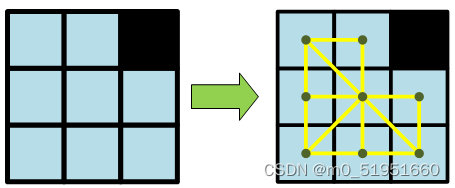
當拓展節點存在障礙物時：
2.3歐幾裏德距離
歐幾裏德距離： D = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 D=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2} D=(x2−x1)2+(y2−y1)2 ，如下圖：
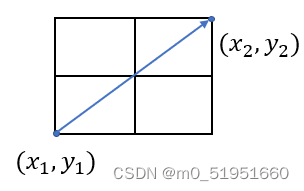
允許朝任何方向移動則可以使用歐幾裏德距離。歐幾裏德距離直接計算兩點之間的距離，更符合實際情況.。
注意：
啓發函數跟拓展方式沒有一定的捆綁關系，上述隻是建議在哪種拓展節點的方式用何種啓發函數。選擇哪種啓發函數取決于應用場景的具體情況，可以根據實際情況進行選擇或者結合多種啓發函數進行綜合考慮。上述部分内容由ChatGPT-plus4.0給出，如有錯誤請大家自行判斷。
三、A*算法的程序實現
1.算法邏輯
1.初始化開始節點S，最終節點G，初始化列表open，closed，初始化全局地圖(網格地圖)
2.從開始節點S出發，把S作爲一個待檢查的方格，放入open列表
3.尋找開始節點S周圍可以到達的方格（最多八個），将它們放入open列表，并設置它們的父節點爲S
4.從“open列表”中删除開始節點S，并将S放入到closed列表中
5.計算每個周圍方格的F值 F=G+H
6.從open列表中選擇F值最小的方格a，将其從open列表放入到closed列表中
7.檢查a所有鄰近的方格
1）障礙物和close列表中的方格不考慮
2）如果這些方格不在open列表中，将它們加入open列表，計算這些方格的F值，并設置父節點爲a
3）如果某相鄰的方格c已經在open列表中，計算新的路徑從S到達方格c（即經過a的路徑）， 判斷是否需要更新父節點和F值：如果新節點c的G值更低，則修改父方格爲方格a，重新計算F值，H值不需要改變（因爲方格到達目标點的預估代價是固定的）,如果新節點c的G值比較高，則說明新的路徑代價更高，則值不做改變（G值不變也不更新）
8.繼續從open列表中找出F值最小的，從open列表中删除，添加到close列表，再繼續找出周圍可以到達的方塊，如此循環
9.結束判斷：當open列表中出現目标方塊G時，說明路徑已找到；當open列表中沒有了數據，說明沒有合适路徑。
2.實驗結果
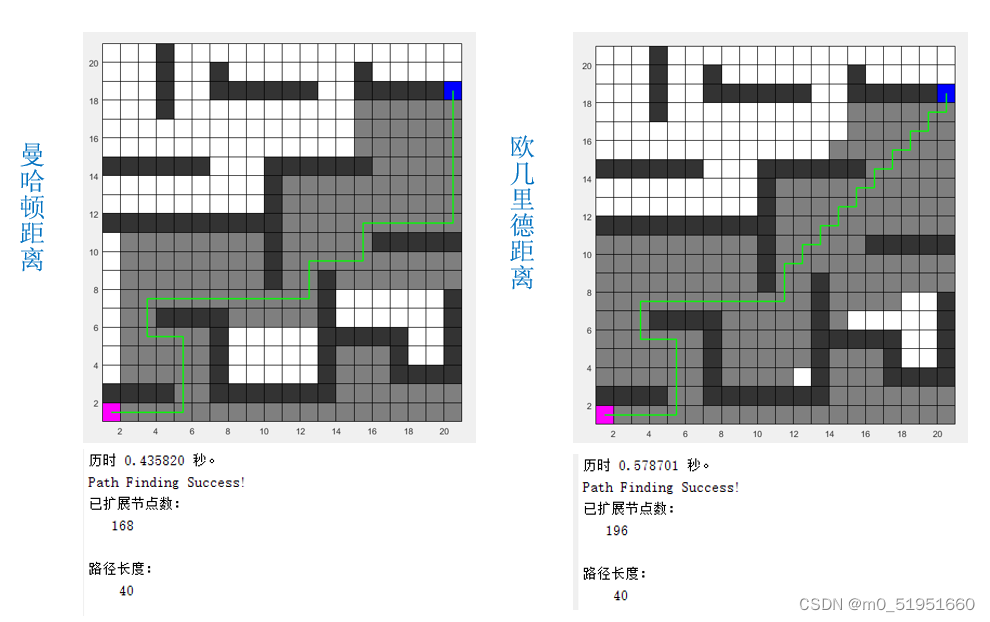
在 20 ∗ 20 20*20 20∗20的栅格地圖中，障礙物自定産生，啓發函數h分别采用曼哈頓距離和歐幾裏德距離，每個節點可以朝四個方向擴展。得到的路徑規劃如左圖。其中陰影部分爲加入過列表（或搜索過）的方格。
當我們增大網格地圖，此時利用A進行路徑規劃又會得到怎麽的結果呢
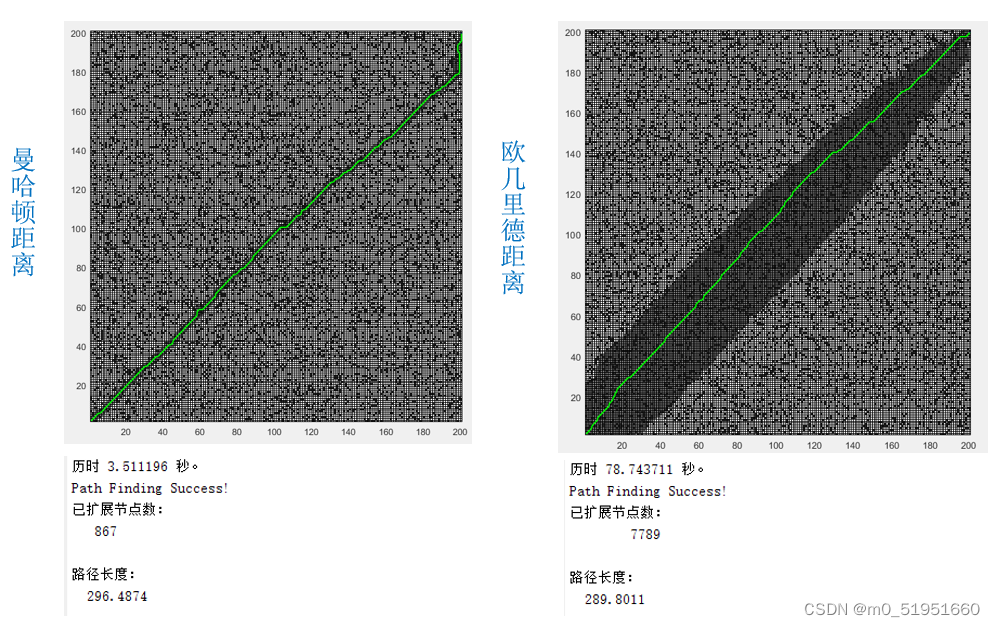在
200
∗
200
200*200
200∗200的栅格地圖中，障礙物随機産生，障礙物覆蓋率占地圖的20%，啓發函數h分别采用曼哈頓距離和歐幾裏德距離，得到的路徑規劃如左圖。A算法的啓發式搜索過程中啓發函數的估計值越接近真實值，規劃效率越高。
在網格地圖中，每個節點可以朝八個方向擴展，此時曼哈頓距離更能準确地反映兩個節點之間的距離。相比之下，歐幾裏德距離計算的H值偏小，同時其需要進行開方運算，耗時較長。
有小夥伴需要程序的可以私我。四、A*算法的總結
A*算法的優缺點
優點：
1.最優性：在滿足一定條件下， A算法能夠保證找到最短路徑。
2.快速性：相對于其他搜索算法， A算法的搜索速度較快，因爲它能夠通過啓發式函數來減少搜索的路徑數。這使得A算法在處理大規模的搜索問題時非常高效。
3.适用性廣泛： A算法可以用于解決各種路徑搜索問題，例如在計算機遊戲中尋找最佳路徑、在機器人導航中尋找最短路徑等等。
缺點：
1.啓發式函數不易設計： A算法需要使用啓發式函數來估算每個節點到目标節點的距離，但是啓發式函數2.的設計并不是一件容易的事情。如果啓發式函數設計不好，那麽搜索效率将會受到很大的影響。
存儲空間占用較大： A算法需要存儲搜索過程中的節點信息，因此當搜索的狀态空間較大時，它需要占用較大的存儲空間。
3.可能陷入局部最優解：雖然A算法能夠保證找到最短路徑，但是當啓發式函數不夠好時， A算法可能會陷入局部最優解，而無法找到全局最優解。
- A*算法的優缺點
