注:此文章的代码推荐在 小熊猫 c + + \boxed{小熊猫c++} 小熊猫c++上运行(使用了EGE图形库)
AI的原理
1.三子棋AI的编写
三子棋的总局面数约为 549 , 946 549,946 549,946,因此我们先以它为基础开始编写。
Test1:构建决策树
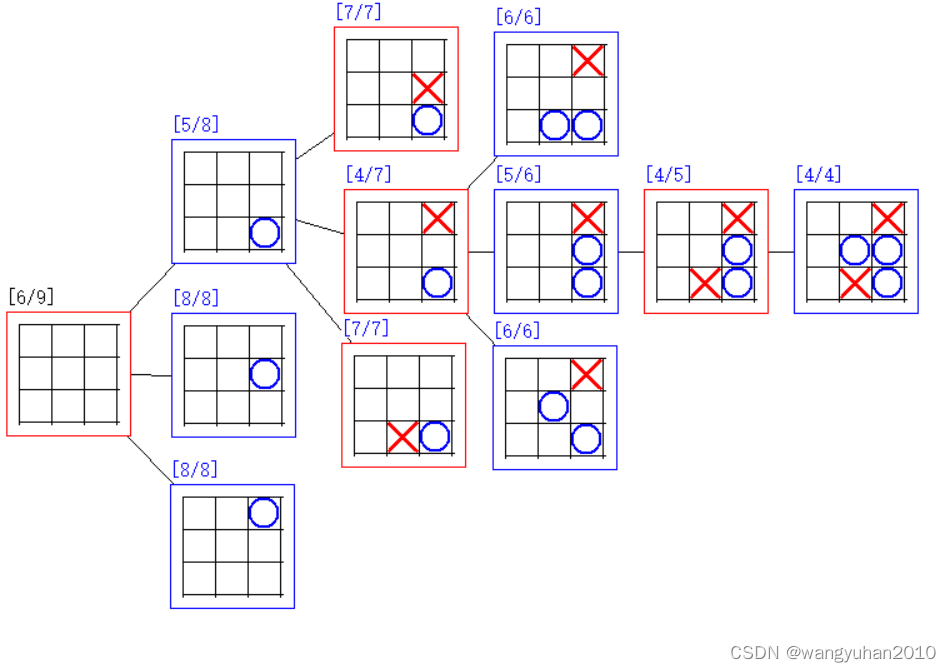
注意:节点上方的 [ a / b ] [a/b] [a/b]表示某个决策下一步还有 b b b种可能,还剩下 a a a种未显示
这里,我们先来讨论某个局面下一步的决策。
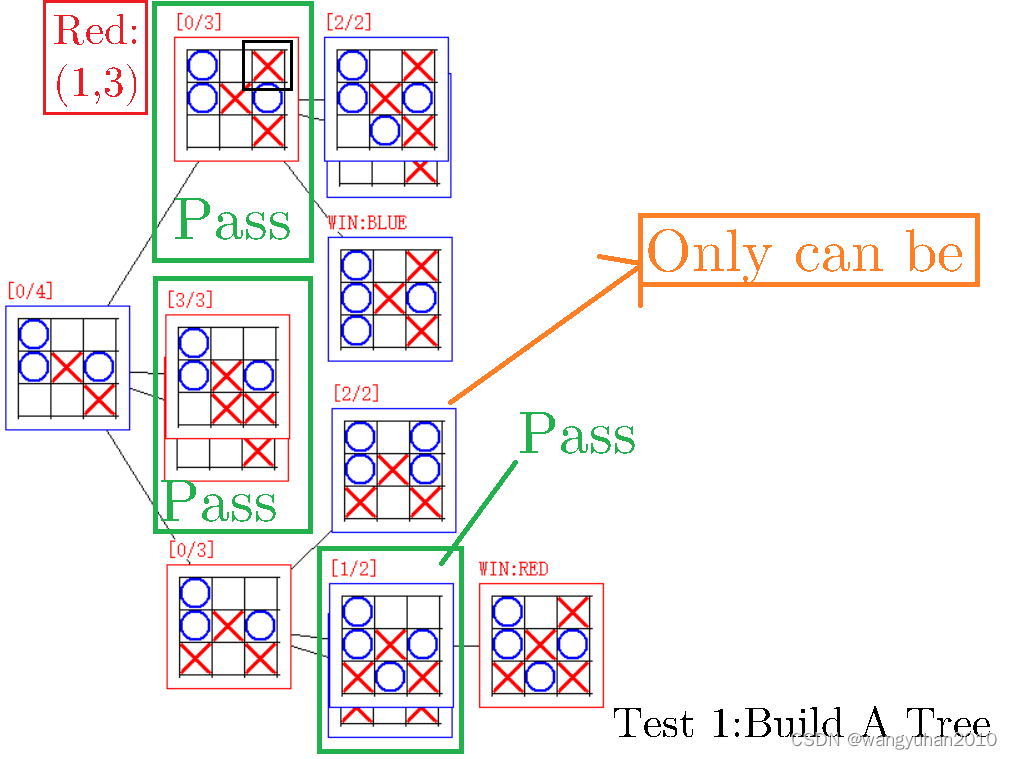
源码见文末 T e s t 1 Test 1 Test1 源码
关注左上红下 ( 1 , 3 ) (1,3) (1,3)的节点,可以发现下一步蓝色可以获胜,那么红方必然不能下 ( 1 , 3 ) (1,3) (1,3)。
同理,红下 ( 3 , 2 ) & ( 1 , 2 ) (3,2)\&(1,2) (3,2)&(1,2)同样不行,只能下 ( 3 , 1 ) (3,1) (3,1)。
继续看蓝方,可以发现蓝方也只能下 ( 1 , 3 ) (1,3) (1,3)
于是,我们就得到了三子棋的AI的博弈树,现在来分析具体方法。
Test2:Min-Max算法
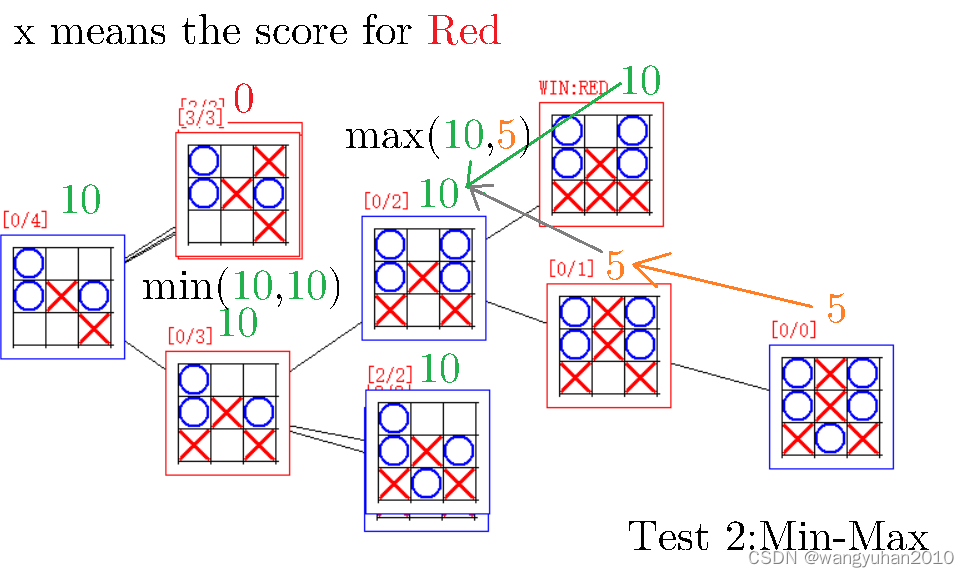
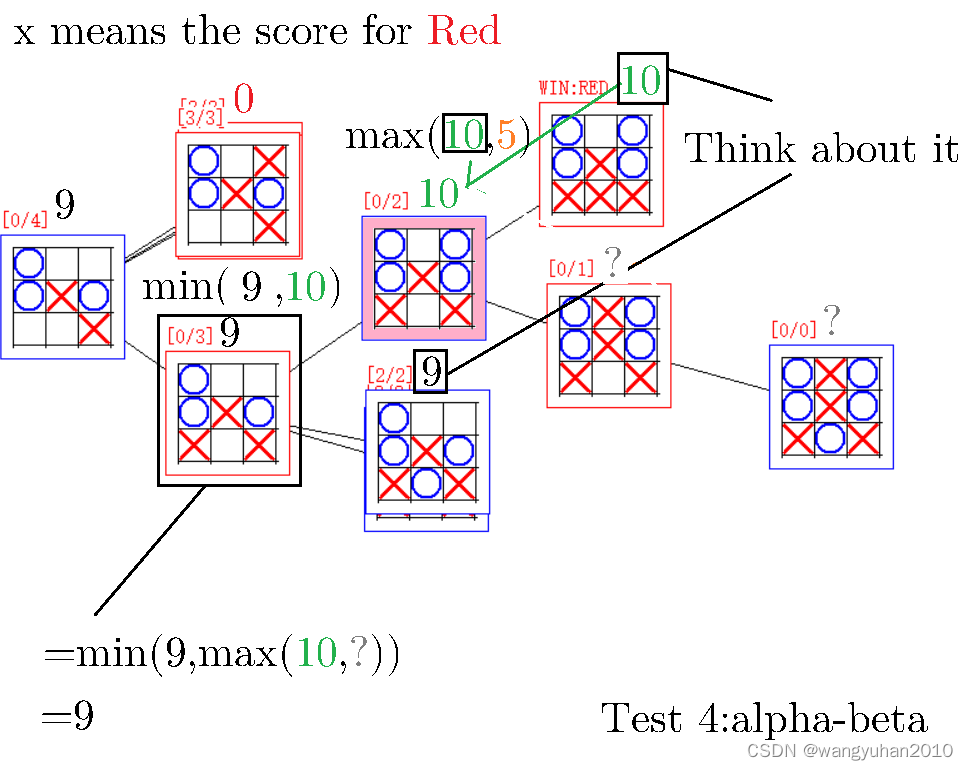
我们将平局定为 5 5 5分,红胜为 10 10 10,红负为 0 0 0分,这样,我们就可以得到每个局面对红方的好处。
设前一步的节点为 u u u,下一步的节点为 v v v
对于每一个蓝点(到蓝色下棋),下一步是红方控制的,当然会选择对自己优的,所以取 V u = max { V v } V_u=\max\{V_v\} Vu=max{Vv},比如下图中粉框节点,下一步红方可以取胜,那当然要选取胜了
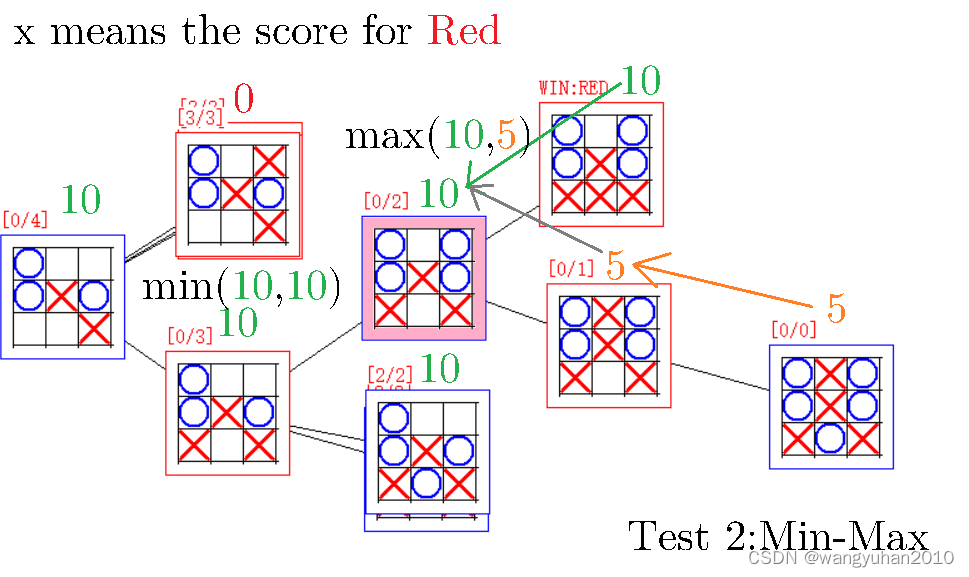
对于每一个红点(到红色下棋),下一步是对方控制的,当然会选择对红方劣的,所以取 V u = min { V v } V_u=\min\{V_v\} Vu=min{Vv},比如如果有一个节点,下一步蓝方可以取胜,那当然要选取胜(红败)了
这样,我们就得到了所有局面的胜率。
源码见文末 T e s t 2 − 1 Test\ 2-1 Test 2−1 源码,AI下3子棋见 T e s t 2 − 2 Test\ 2-2 Test 2−2 源码
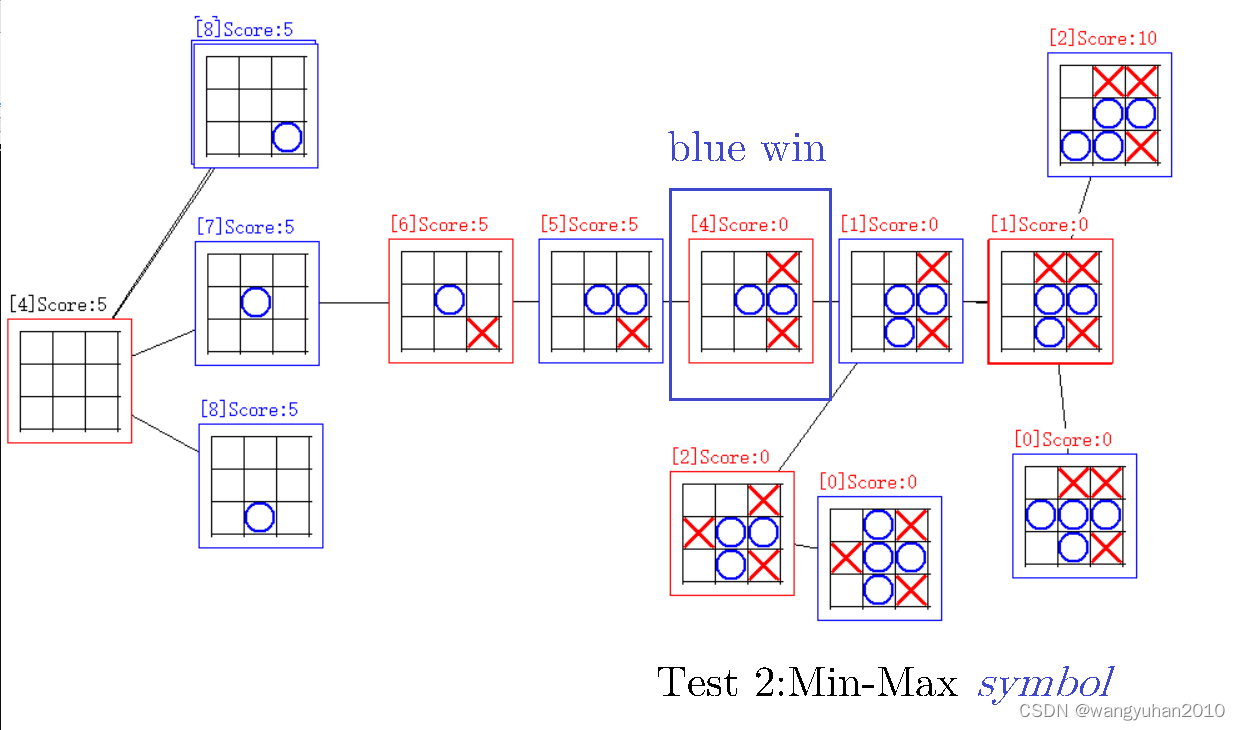
当然,经过对所有局面的考察,可以发现没有必胜的可能,但是还是有可能在前几步利用对手失误获得必胜(读者可以自行查看程序),如上图。
1.五子棋AI的编写
五子棋的总局面数约为 1 0 50 10^{50} 1050,因此不可能构造完整的决策树。
Test3:对局面进行估分
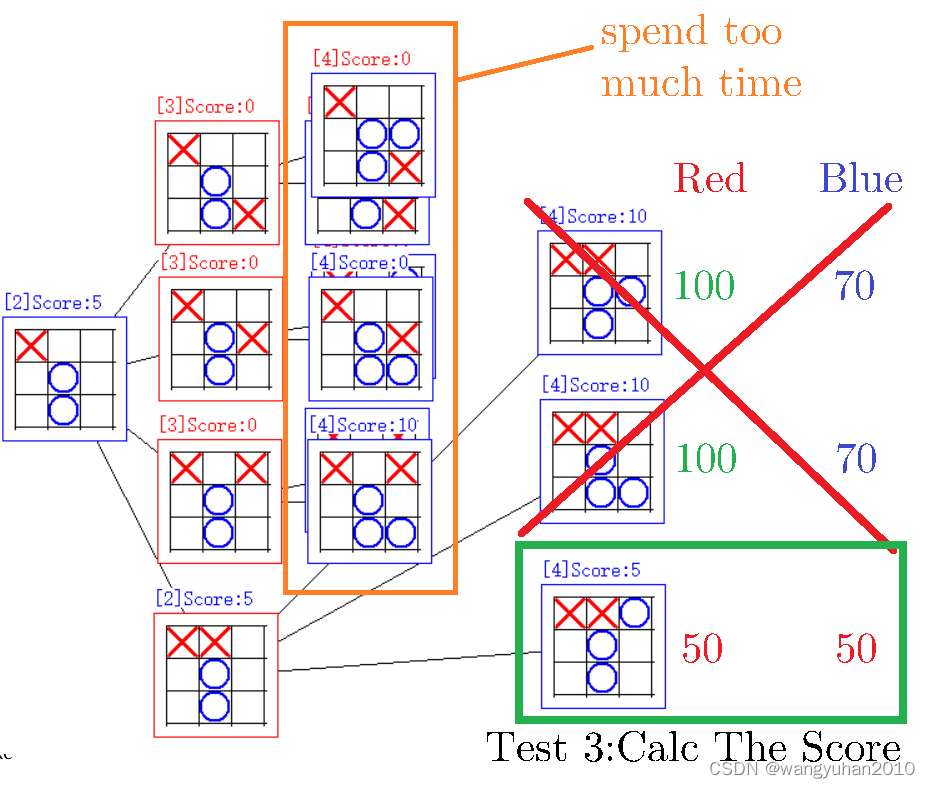
还是以三子棋为例,把 [ X ] [ X ] [ ] [X][X][\ \ \ ] [X][X][ ]记为 50 50 50分, [ ] [ X ] [ ] [\ \ \ ][X][\ \ \ ] [ ][X][ ]和 [ ] [ ] [ X ] [\ \ \ ][\ \ \ ][X] [ ][ ][X]记为 10 10 10分, [ X ] [ X ] [ X ] [X][X][X] [X][X][X]记为 100 100 100分,就可以在决策树层数较少的情况估算价值。
有了估值,AI就智慧多了,如果我们把比较有可能的点(这里是选前2个)单独挑出来,其余的点不进行展开,可以发现它已经把较优的点选好了(如上图),就会大大减少节点数。
以下是一次对局:(AI:蓝)
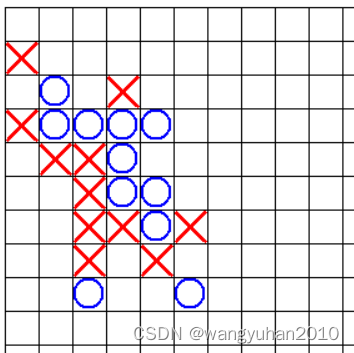
评价:目光较短浅,但是速度非常快(约0.3s)
源码见 T e s t 3 Test \ 3 Test 3
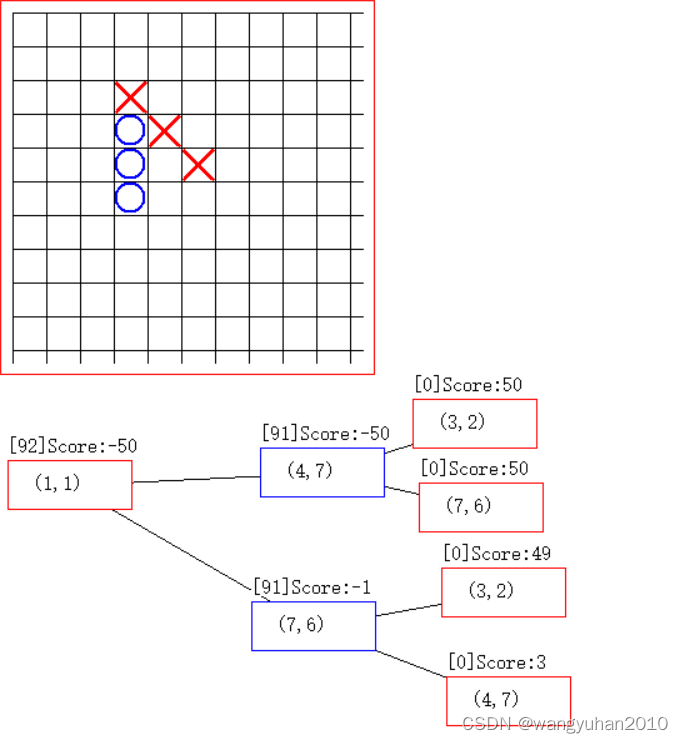
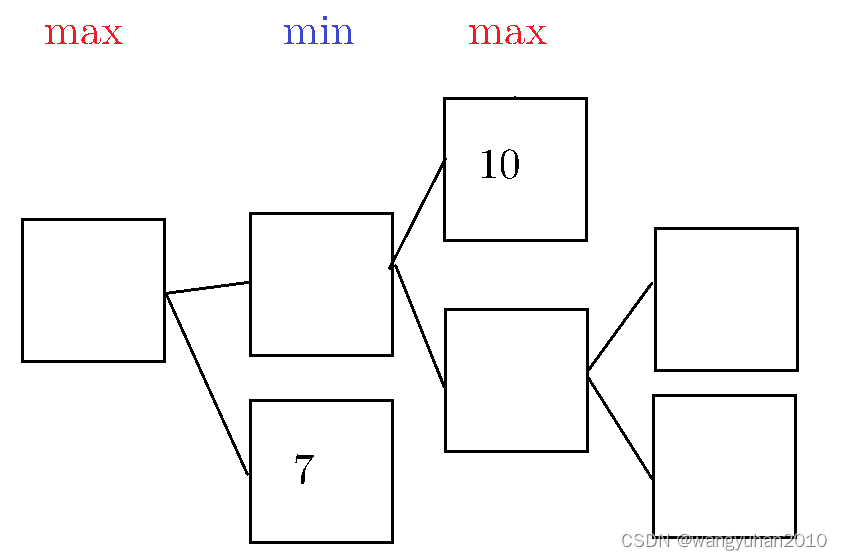
Test4:α-β剪枝
AI不行,就加深度,时间太长,就加剪枝
发现 V u = m a x { m i n { a , b } , c } V_u=max\{min\{a,b\},c\} Vu=max{min{a,b},c}时,如果 a & b a\&b a&b有一个 c, V u V_u Vu就是 c c c
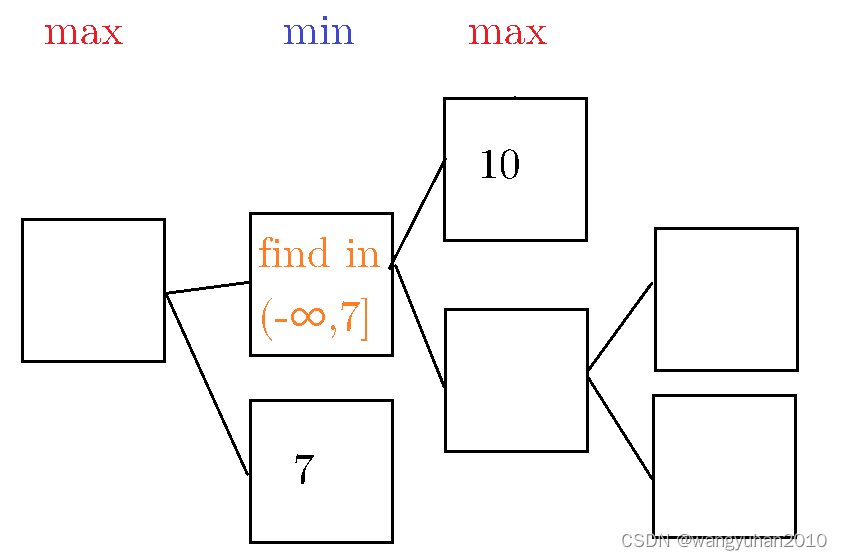
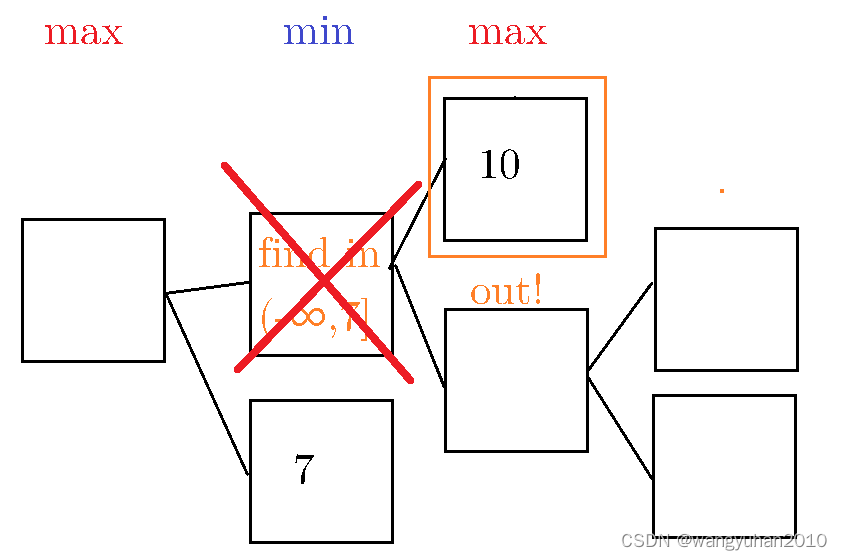
即: m i n ( 7 , m a x ( 10 , ? ) ) = 7 min(7,max(10,?))=7 min(7,max(10,?))=7
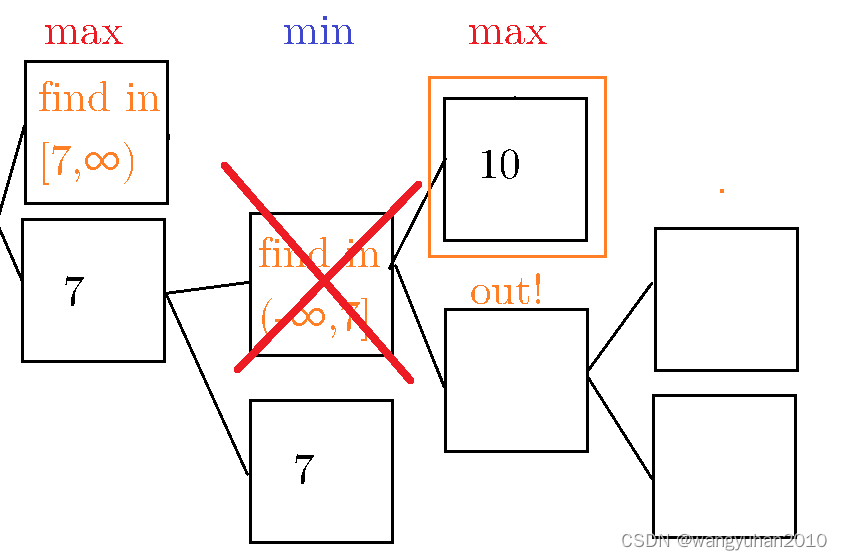
(实测大约剪掉了 3 / 4 3/4 3/4的节点,效率不太高,所以笔者并没有用)
本文中所有源代码
T e s t 1 Test \ 1 Test 1
#include
#include
#include
using namespace std;
struct BOARD{int a[3][3];int number,win;};
struct SHOW{int x,y;int SON;}node[4020889];
int NODE=1;bool show[4028089];
BOARD tree[4028809];
vectorson[4002889];
int mx,my,Dl,LINE[400288][5],LN,Dr,LOCK,Rc=1;
int check(BOARD now)
{
for(int i=0;i{1, 0}, {0, 1}, {1, 1}, {1, -1}};
int score = 0;
for (int i = 0; i 








