【机器学习吴恩达】2022课程笔记（持续更新）-慈云数据

一、机器学习

1.1 机器学习定义

计算机程序从经验E中学习，解决某一任务T，进行某一性能P，通过P测定在T上的表现因经验E而提高

eg：跳棋程序

E：程序自身下的上万盘棋局

T：下跳棋

P：与新对手下跳棋时赢的概率

1.2 监督学习 supervised learning

1.2.1 监督学习定义

给算法一个数据集，其中包含了正确答案，算法的目的是给出更多的正确答案

如预测房价（回归问题）、肿瘤良性恶性分类（分类问题）

1.3 无监督学习 unsupervised learning

1.3.1 无监督学习定义

只给算法一个数据集，但是不给数据集的正确答案，由算法自行分类。

如聚类

1.谷歌新闻每天收集几十万条新闻，并按主题分好类

2.市场通过对用户进行分类，确定目标用户

3.鸡尾酒算法：两个麦克风分别离两个人不同距离，录制两段录音，将两个人的声音分离开来（只需一行代码就可实现，但实现的过程要花大量的时间）

1.3.2 聚类算法

二、单变量的线性回归 univariate linear regression——预测问题

2.1 单变量线性函数

假设函数 hθ(x) = θ0 + θ1x

代价函数平方误差函数或者平方误差代价函数

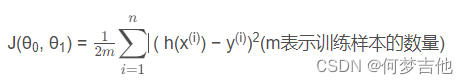
在这里插入图片描述

h(x(i))是预测值，也写做y帽，y(i)是实际值，两者取差

分母的2是为了后续求偏导更好计算。

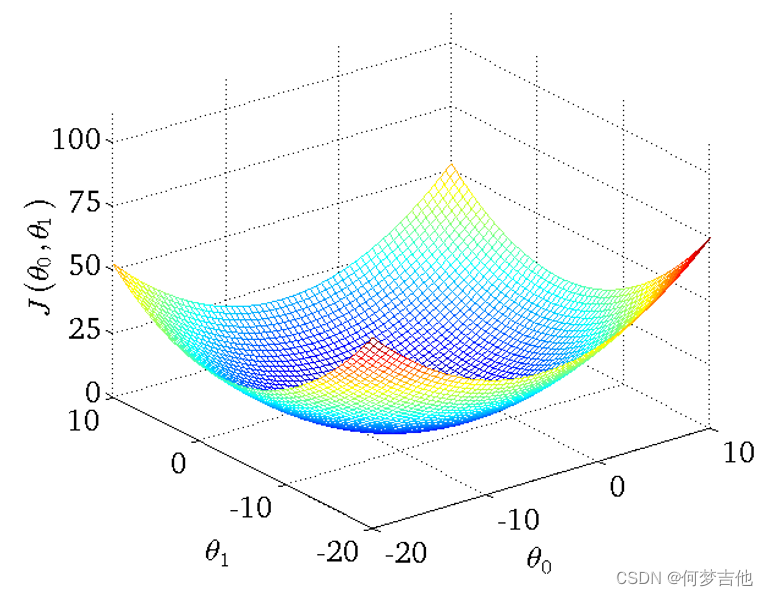
目标：最小化代价函数，即minimize J(θ0, θ1)

得到的代价函数的三维图如下
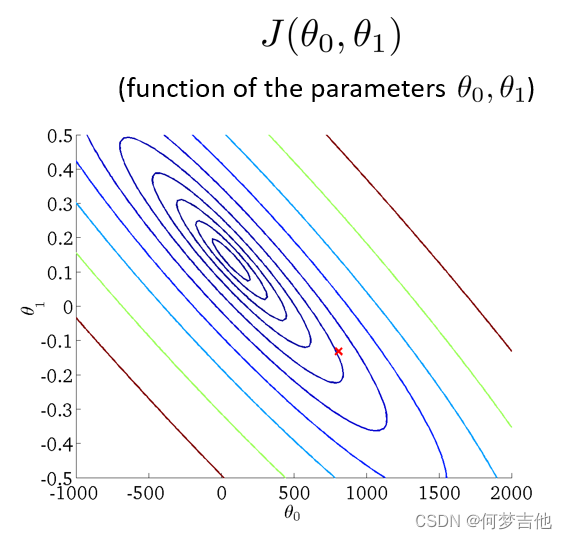
将三维图平面化等高线图 contour plot
等高线的中心对应最小代价函数
2.2 梯度下降算法 Gradient Descent algorithm

算法思路
- 指定θ0 和 θ1的初始值
- 不断改变θ0和θ1的值，使J(θ0,θ1)不断减小
- 得到一个最小值或局部最小值时停止
  梯度：函数中某一点(x, y)的梯度代表函数在该点变化最快的方向
  （选用不同的点开始可能达到另一个局部最小值）
  
  梯度下降公式
  - θ0和θ1应同步更新，否则如果先更新θ0，会使得θ1是根据更新后的θ0去更新的，与正确结果不相符
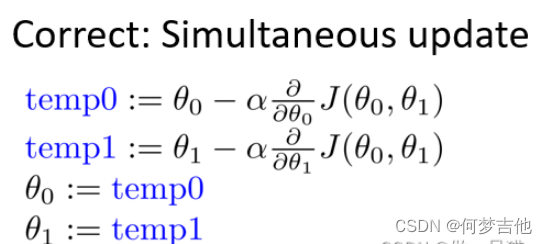
  - 原理：偏导表示的是斜率，斜率在最低点左边为负，最低点右边为正。在移动过程中，偏导值会不断变小，进而移动的步幅也不断变小，最后不断收敛直到到达最低点；在最低点处偏导值为0，不再移动
    
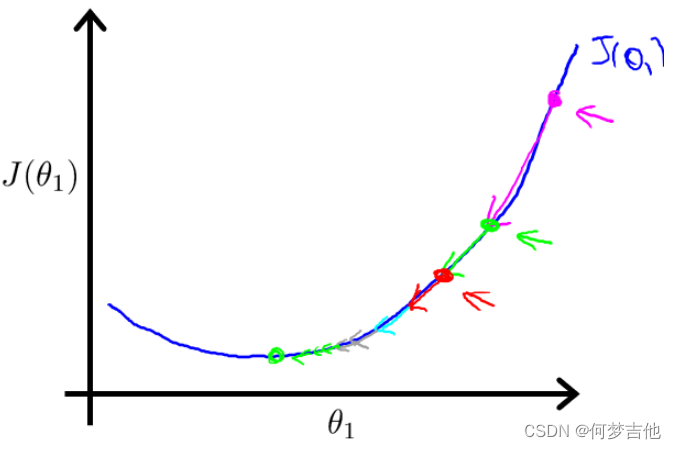
    关于α的选择
    如果α选择太小，会导致每次移动的步幅都很小，最终需要很多步才能最终收敛
    如果α选择太大，会导致每次移动的步幅过大，可能会越过最小值，无法收敛甚至会发散
    
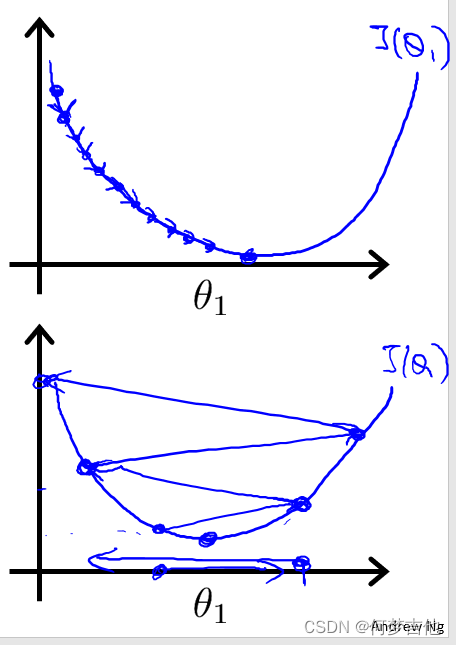
    2.3 用于线性回归的梯度下降 ——Batch梯度下降
    - 公式推导
    - 梯度回归的局限性：可能得到的是局部最优解
      线性回归的梯度下降的函数是凸函数，bowl shape，因此没有局部最优解，只有全局最优解
      拓展：凸函数与凹函数
    - 批量梯度下降代码实现
      批处理是指在一次迭代中运行所有的例子
      验证梯度下降是否正常工作的一个好方法是看一下𝐽(𝑤,𝑏)的值。
      并检查它是否每一步都在减少
```
def gradient_descent(x, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): 
    """
    Performs batch gradient descent to learn theta. Updates theta by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x :    (ndarray): Shape (m,)
      y :    (ndarray): Shape (m,)
      w_in, b_in : (scalar) Initial values of parameters of the model
      cost_function: function to compute cost
      gradient_function: function to compute the gradient
      alpha : (float) Learning rate
      num_iters : (int) number of iterations to run gradient descent
    Returns
      w : (ndarray): Shape (1,) Updated values of parameters of the model after
          running gradient descent
      b : (scalar)                Updated value of parameter of the model after
          running gradient descent
    """
    
    # number of training examples
    m = len(x)
    
    # An array to store cost J and w's at each iteration — primarily for graphing later
    J_history = []
    w_history = []
    w = copy.deepcopy(w_in)  #avoid modifying global w within function
    b = b_in
    
    for i in range(num_iters):
        # Calculate the gradient and update the parameters
        dj_dw, dj_db = gradient_function(x, y, w, b )  
        # Update Parameters using w, b, alpha and gradient
        w = w - alpha * dj_dw               
        b = b - alpha * dj_db               
        # Save cost J at each iteration
        if i
```