1.算法简介
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,簇集的划定完全由样本的聚集程度决定。聚集程度不足以构成簇落的那些样本视为噪声点,因此DBSCAN聚类的方式也可以用于异常点的检测。
2.算法原理
2.1 基本原理
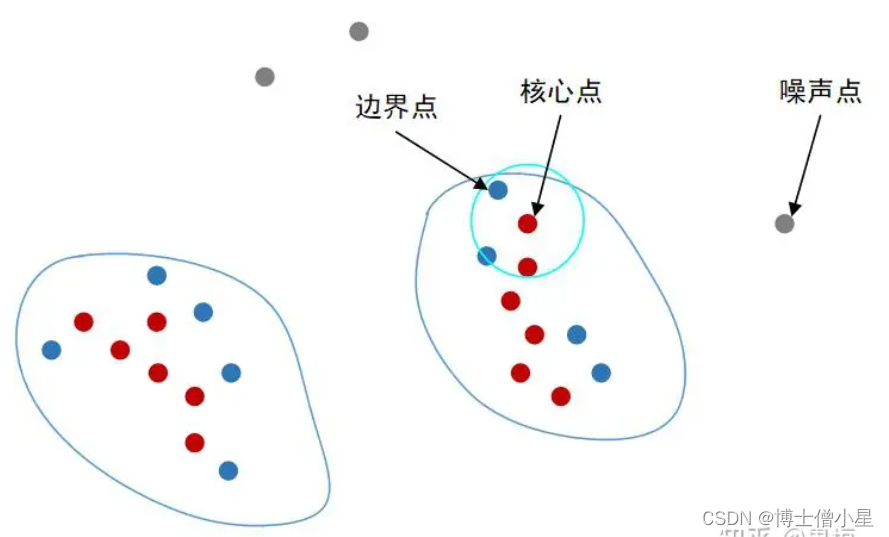
算法的关键在于样本的‘聚集程度’,这个程度的刻画可以由聚集半径和最小聚集数两个参数来描述。如果一个样本聚集半径领域内的样本数达到了最小聚集数,那么它所在区域就是密集的,就可以围绕该样本生成簇落,这样的样本被称为核心点。如果一个样本在某个核心点的聚集半径领域内,但其本身又不是核心点,则被称为边界点;既不是核心点也不是边界点的样本即为噪声点。其中,最小聚集数通常由经验指定,一般是数据维数+1或者数据维数的2倍。
通俗地讲,核心点就是构成一个簇落的核心成员;边界点就是构成一个簇落的非核心成员,它们分布于簇落的边界区域;噪声点是无法归属在任何一个簇集的游离的异常样本。如图所示。
对于聚成的簇集,这里有三个相关的概念:密度直达,密度可达,密度相连。
- 密度直达:对一个核心点p,它的聚集半径领域内的有点q,那么称p到q密度直达。密度直达不具有对称性。
- 密度可达: 有核心点p1,p2,…,pn,非核心点q,如果pi到pi+1(i=1,2,…,n-1)是密度直达的,pn到q是密度直达的,那么称核心点pi(i=1,2,…,n)到其他的点是密度可达的。密度可达不具有对称性。
- 密度相连:如果有核心点P,到两个点A和B都密度可达,那么称A和B密度相连。密度相连具有对称性。
简单地讲,核心点到其半径邻域内的点是密度直达的;核心点到其同簇集内的点是密度可达的;同一个簇集里的成员间是密度相连的。
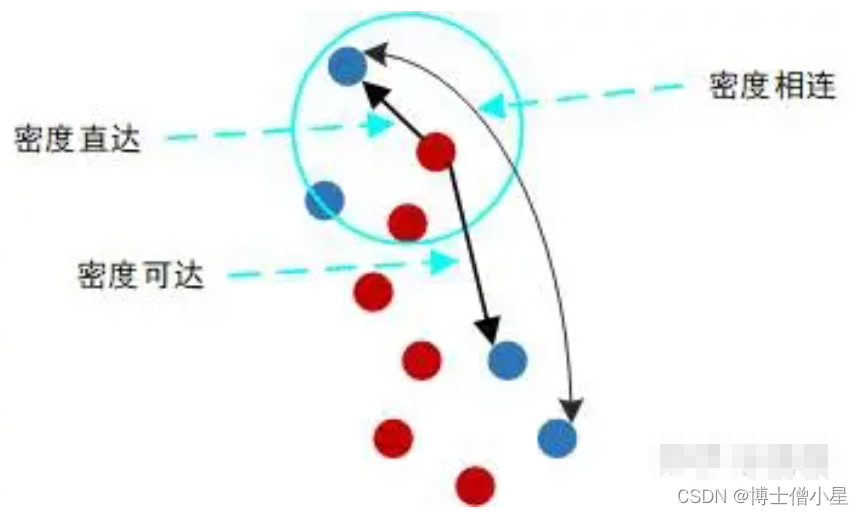
由定义易知,密度直达一定密度可达,密度可达一定密度相连。密度相连就是对聚成的一个簇集最直接的描述。
2.2 算法描述
输入:样本集D,聚集半径r,最小聚集数MinPts;
输出:簇集C1,C2,…,Cn,噪声集O.
根据样本聚集程度,传播式地划定聚类簇,并将不属于任何一个簇的样本划入噪声集合。
- (1)随机搜寻一个核心点p,

- (2)在核心点p处建立簇C,将r邻域内所有的点加入簇C.
- (3)对邻域内所有未被标记的点迭代式进行考察,扩展簇集.若一个邻域点q为核心点,则将它领域内未归入集合的点加入簇C中.
- (4)重复以上步骤,直至所有样本划入了指定集合;
- (5)输出簇集C1,C2,…,Cn和噪声集合O。
3.优缺点
3.1 优势
1.可以发现任意形状的簇,适用于非凸数据集;
2.可以进行异常检测;
3.不需要指定簇数,根据样本的密集程度适应性地聚集。
3.2 不足
1.当样本集密度不均匀,不同簇中的平均密度相差较大时,效果较差;
2.聚集半径和最小聚集数两个参数需人工指定。
4.示例
假设二维空间中有下列样本,坐标为(1,2),(1,3),(3,1),(2,2),(9,8),(8,9),(9,9),(18,18)
由DBSCAN算法完成聚类操作。
过程演算:
由经验指定参数聚集半径r=2,最小聚集数MinPts=3。
- (1)随机搜寻一个核心点,若不存在,返回噪声集合。考察点(1,2),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共三个样本点,达到了MinPts数,因此(1,2)为核心点。
- (2)在核心点(1,2)处建立簇C1,原始簇成员为r邻域内样本:(1,2)、(1,3)、(2,2)。
- (3)对簇落C1成员迭代式进行考察,扩展簇集。先考察(1,3),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共三个样本点,达到了MinPts数,因此(1,3)为核心点,它邻域内的样本均已在簇C1中,无需进行操作。
再考察(2,2),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共四个样本点,达到了MinPts数,因此(2,2)为核心点,将它领域内尚未归入任何一个簇落的点(3,1)加入簇C1。
再考察(3,1),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共两个样本点,因此(3,1)是非核心点。
考察结束,簇集C1扩展完毕。
- (4)在其余未归簇的样本点中搜寻一个核心点,若不存在,返回噪声集合。考察点(9,8),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共三个样本点,达到了MinPts数,因此(9,8)为核心点。
- (5)在核心点(9,8)处建立簇C2,原始簇成员为r邻域内样本:(9,8)、(8,9)、(9,9)。
- (6)对簇落C2成员迭代式进行考察,扩展簇集。先考察(8,9),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共三个样本点,达到了MinPts数,因此(8,9)为核心点,它邻域内的样本均已在簇C2中,无需进行操作。
再考察(9,9),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共三个样本点,达到了MinPts数,因此(9,9)为核心点。它邻域内的样本均已在簇C2中,无需进行操作。
考察结束,簇集C2扩展完毕。
- (7)在其余未归簇的样本点中搜寻一个核心点,若不存在,返回噪声集合。其余未归簇的样本点集合为{(18,18)},考察(18,18),它到各点的距离分别为

在它的r邻域内,包括了自身在内的共一个样本点,未达到MinPts数,因此(18,18)为非核心点。其余未归簇的样本中不存在核心点,因此归入噪声集O={(18,18)}。
- (8)输出聚类结果
簇类C1:{(1,2),(1,3),(3,1),(2,2)}
簇类C2:{(9,8),(8,9),(9,9)}
噪声集O:{(18,18)}
5.Python代码
''' 功能:用Python实现DBSCAN聚类算法。 ''' from sklearn.cluster import DBSCAN import numpy as np import matplotlib.pyplot as plt # 初始化数据 data = np.array([(1,2),(1,3),(3,1),(2,2), (9,8),(8,9),(9,9), (18,18)]) # 定义DBSCAN模型 dbscan = DBSCAN(eps=2,min_samples=3) # 计算数据,获取标签 labels = dbscan.fit_predict(data) # 定义颜色列表 colors = ['b','r','c'] T = [colors[i] for i in labels] # 输出簇类 print('\n 聚类结果: \n') ue = np.unique(labels) for i in range(ue.size): CLS = [] for k in range(labels.size): if labels[k] == ue[i]: CLS.append(tuple(data[k])) print('簇类{}:'.format(ue[i]),CLS) # 结果可视化 plt.figure() plt.scatter(data[:,0],data[:,1],c=T,alpha=0.5) # 绘制数据点 plt.show()
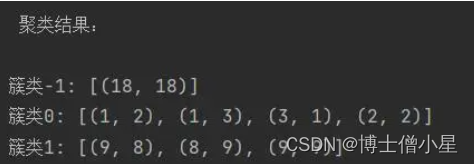

- (8)输出聚类结果
- (7)在其余未归簇的样本点中搜寻一个核心点,若不存在,返回噪声集合。其余未归簇的样本点集合为{(18,18)},考察(18,18),它到各点的距离分别为
- (4)在其余未归簇的样本点中搜寻一个核心点,若不存在,返回噪声集合。考察点(9,8),它到各点的距离分别为
- (1)随机搜寻一个核心点,若不存在,返回噪声集合。考察点(1,2),它到各点的距离分别为
- (1)随机搜寻一个核心点p,









