文章目录
- 标准化流程
- 平行假设检验
- 效果评估
- 安慰剂检验
标准化流程
此前的文章介绍了双重差分法(difference-in-differences,DID)的原理,并说明了其是算法策略效果评估的有效方案之一。本文将主要描述DID的标准化流程,以及如何使用stata代码实现全流程。
先上标准化流程的全景图,然后再逐一理解。作为对比,此前文章里的代码只是实现了第二层中的“基本DID”模块。

在标准化流程中,一共包含三个模块:第一个模块是平行假设检验,主要任务是确保对照组和实验组在算法策略干预前,指标的变化趋势相同,这是DID的最基本前提;第二个模块是效果评估,旨在通过DID的演算,量化算法策略对指标的影响和显著性水平;第三个模块是安慰剂检验,其目标是检验效果评估模型中的结果是否受到了其他因素的影响。
安慰剂检验,这个名字乍一看,挺奇怪的,稍微解释一下。安慰剂多用于医学,通常是指病人虽然获得无效的治疗,但却让其 “预料” 或 “相信” 治疗有效,而让病患症状得到舒缓的现象。此处使用主要是为了避免实验组出现安慰剂效应,影响实验结果。
平行假设检验
绘制趋势图就是把对照组和实验组指标的历史变化趋势绘制出来,然后根据个人经验判断两者的变化趋势是否相同。该方法较为主观,不符合理工科的严谨习惯,因此本节主要介绍事件研究法。
先回顾一下DID的基本模型
Y i t = α + δ D i + λ T t + β ( D i × T t ) + ϵ i t Y_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\epsilon_{it} Yit=α+δDi+λTt+β(Di×Tt)+ϵit
为了做平行假设检验,需要将模型调整为
Y i t = α + δ D i + λ T t + β ( D i × T t ) + ∑ μ i ⋅ y e a r i × D i + ϵ i t Y_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\sum{\mu_i·year_i \times D_i}+\epsilon_{it} Yit=α+δDi+λTt+β(Di×Tt)+∑μi⋅yeari×Di+ϵit
相比基本模型,该项多了 ∑ μ i ⋅ y e a r i × D i \sum{\mu_i·year_i \times D_i} ∑μi⋅yeari×Di。此处, y e a r i year_i yeari为时间虚拟变量,当年观测年为1,其他年份为0; μ i \mu_i μi是对应的系数值。
做平行假设检验,主要看 μ i \mu_i μi是否显著不为0:如果至少一个值显著不为0,那么认为不满足平行假设检验;反之,则满足平行假设检验。
本文使用普林斯顿大学构造的DID数据:A、B、C、D、E、F和G是非常相似的7个地区,E、F和G三地在1994年实行了一项新政策,而A、B、C和D则没有实行,目标是评估新政策对指标y的影响。
以下为政策实施前的数据:
以下代码可以实现对 μ i \mu_i μi的计算,并且绘制平行检验的结果。
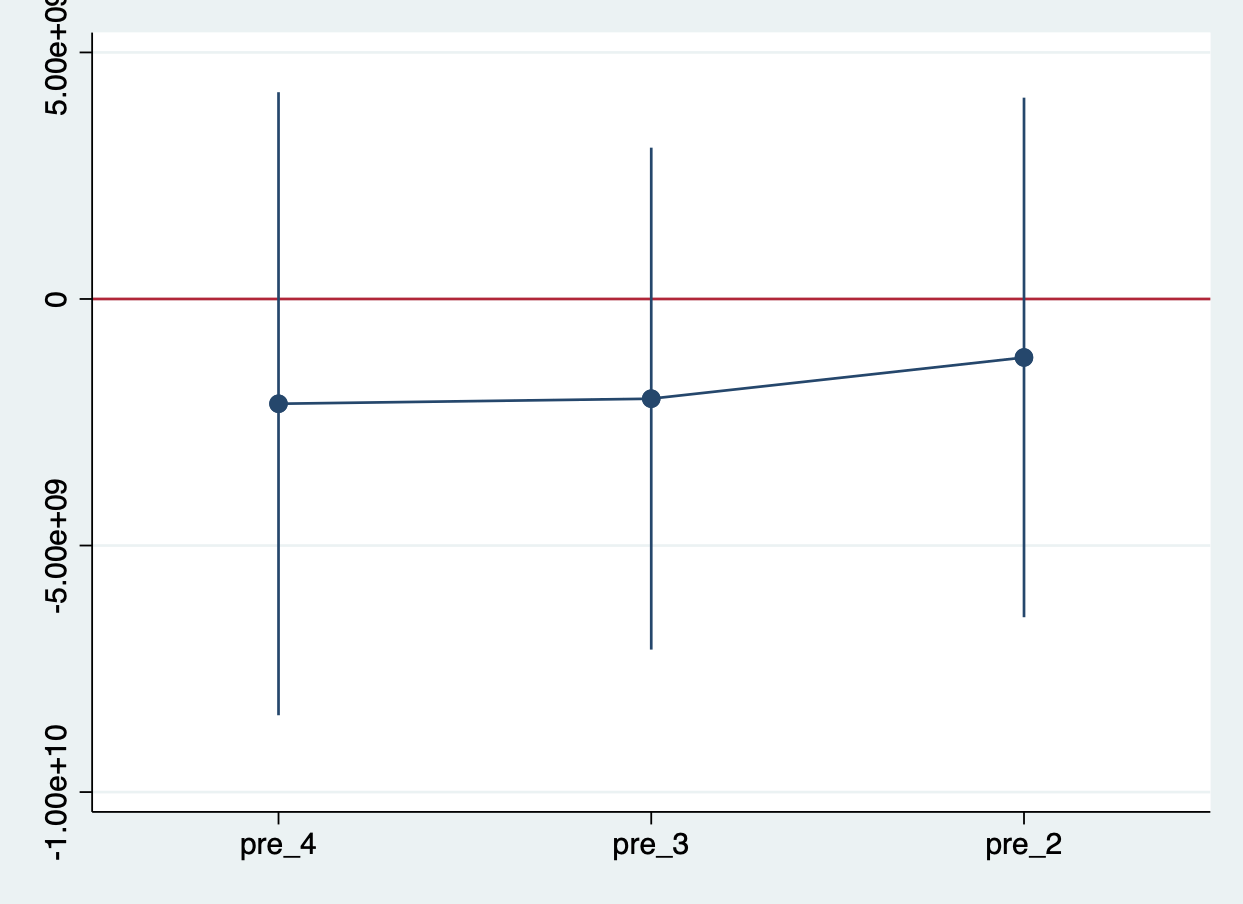
gen period = (year>=1994) & !missing(year) // 生成时间虚拟变量,1994年前为0,反之为1 gen treat = (country>4) & !missing(country) // 生成区域的虚拟变量,干预为1,反之为0 gen did = period * treat // 生成交叉项 // 如果i = 1(1)4,后续绘图时,pre_i的顺序会不一致 gen policy = year - 1994 forvalues i = 4(-1)1{ gen pre_`i' = (policy == -`i' & treat == 1) } // 回归计算 xtreg y pre_*, fe r // 绘制曲线图 est sto reg coefplot reg, keep(pre_*) vertical recast(connect) yline(0)先看一下 μ i \mu_i μi的结算结果:分别对应pre_4、pre_3和pre_2行、P>|t|列的数值,即0.442,0.369和0.602。这三个值均大于0.05,所以满足平行假设检验。
Fixed-effects (within) regression Number of obs = 28 Group variable: country Number of groups = 7 R-sq: Obs per group: within = 0.0673 min = 4 between = 0.2121 avg = 4.0 overall = 0.0118 max = 4 F(2,6) = . corr(u_i, Xb) = -0.5136 Prob > F = . (Std. Err. adjusted for 7 clusters in country) ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- pre_4 | -2.12e+09 2.58e+09 -0.82 0.442 -8.44e+09 4.19e+09 pre_3 | -2.02e+09 2.08e+09 -0.97 0.369 -7.11e+09 3.07e+09 pre_2 | -1.19e+09 2.15e+09 -0.55 0.602 -6.45e+09 4.08e+09 pre_1 | 0 (omitted) _cons | 1.69e+09 7.04e+08 2.40 0.053 -3.23e+07 3.41e+09 -------------+---------------------------------------------------------------- sigma_u | 2.472e+09 sigma_e | 2.588e+09 rho | .4771219 (fraction of variance due to u_i) ------------------------------------------------------------------------------我们还可以看一下pre_4、pre_3和pre_2行,[95% Conf. Interval]两列的数据,下图绘制了这两列数据的范围。显然,都包含了0值,即通过了平行假设检验。
此处做一下额外说明:本节只使用政策干预前的数据做平行假设检验,而很多文献则是把干预前和干预后数据放在一起做平行假设检验,但是个人认为后者是不合理的,主要原因是:我们在实际操作时,需要先通过平行假设检验找出合适的对照组和实验组,然后再去做实验,此时并没有干预后数据。
接下来搞点事情:调整treat值,和之前恰好相反。然后再重新做一遍平行假设检验。
原理上来说,只是互换了实验组和对照组的身份,平行假设检验的结果应该是不变的。
gen period = (year>=1994) & !missing(year) gen treat = (country|t|值为0.006,小于0.05;[95% Conf. Interval]也已不包含0。即不再满足平行假设检验。
这和我们的直观认知是不符的。但是具体原因暂时并未探查到,如遇大神,望能不吝赐教。
Fixed-effects (within) regression Number of obs = 28 Group variable: country Number of groups = 7 R-sq: Obs per group: within = 0.3044 min = 4 between = 0.2121 avg = 4.0 overall = 0.2536 max = 4 F(3,6) = 53.56 corr(u_i, Xb) = -0.1823 Prob > F = 0.0001 (Std. Err. adjusted for 7 clusters in country) ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- pre_4 | -4.00e+09 1.70e+09 -2.36 0.057 -8.16e+09 1.56e+08 pre_3 | -3.00e+09 1.33e+09 -2.26 0.064 -6.25e+09 2.47e+08 pre_2 | -3.58e+09 8.62e+08 -4.15 0.006 -5.68e+09 -1.47e+09 pre_1 | 0 (omitted) _cons | 2.63e+09 3.44e+08 7.64 0.000 1.79e+09 3.47e+09 -------------+---------------------------------------------------------------- sigma_u | 1.888e+09 sigma_e | 2.235e+09 rho | .41645141 (fraction of variance due to u_i) ------------------------------------------------------------------------------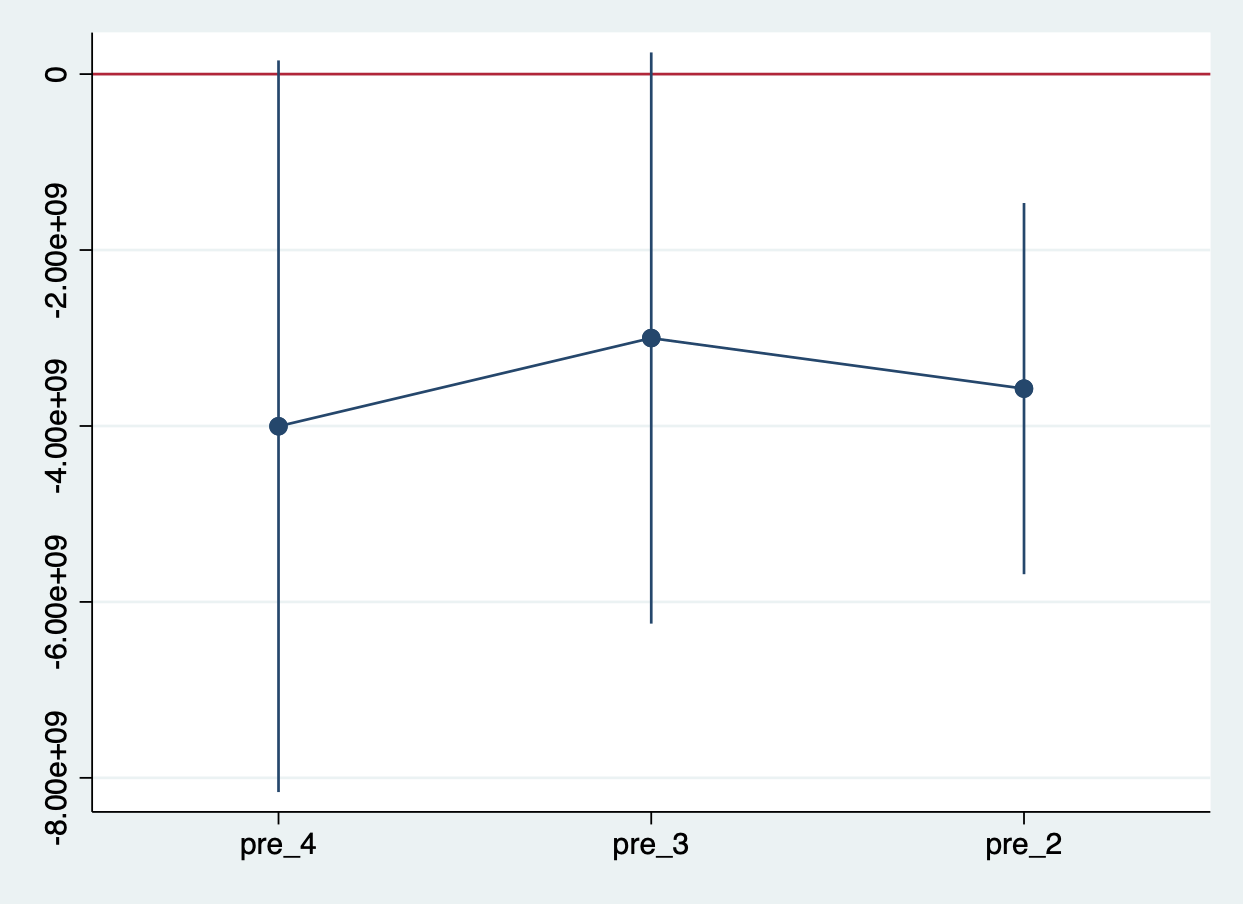
效果评估
以下为政策实施后的数据。

文章中已经实现过基本DID,因此本节直接给出代码。相比之前代码,DID回归步骤使用reg方式替代了diff方式。两种方式都可以,不过reg更常用。
gen period = (year>=1994) & !missing(year) // 生成时间虚拟变量,1994年前为0,反之为1 gen treat = (country>4) & !missing(country) // 生成区域的虚拟变量,干预为1,反之为0 gen did = period * treat // 生成交叉项 reg y period treat did, r //DID回归:reg方式
从结果看,did行、P>|t|列的值( β \beta β)为0.088,大于0.05,即政策效果不显著。
Linear regression Number of obs = 70 F(3, 66) = 2.17 Prob > F = 0.0998 R-squared = 0.0827 Root MSE = 3.0e+09 ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- period | 2.29e+09 9.00e+08 2.54 0.013 4.92e+08 4.09e+09 treat | 1.78e+09 1.05e+09 1.70 0.094 -3.11e+08 3.86e+09 did | -2.52e+09 1.45e+09 -1.73 0.088 -5.42e+09 3.81e+08 _cons | 3.58e+08 7.61e+08 0.47 0.640 -1.16e+09 1.88e+09 ------------------------------------------------------------------------------除了以上的基本DID,还可以在模型中添加其他控制变量,例如:x1-x3、opinion和country
reg y period treat did x1-x3 i.opinion i.country, r
此时, β \beta β值变为0.01,即政策效果变得显著。查看控制变量的系数后可知,变量 x 1 x_1 x1的交叉项系数也为0.01,即对政策影响较大。
Linear regression Number of obs = 70 F(14, 55) = 3.32 Prob > F = 0.0007 R-squared = 0.3800 Root MSE = 2.7e+09 ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- period | 1.63e+09 8.16e+08 2.00 0.050 -970567.3 3.27e+09 treat | -5.13e+08 2.51e+09 -0.20 0.839 -5.54e+09 4.52e+09 did | -3.67e+09 1.37e+09 -2.67 0.010 -6.42e+09 -9.13e+08 x1 | 2.86e+09 1.07e+09 2.67 0.010 7.12e+08 5.00e+09 x2 | 3021459 2.43e+09 0.00 0.999 -4.88e+09 4.88e+09 x3 | 3.17e+08 3.09e+08 1.03 0.310 -3.03e+08 9.37e+08 | opinion | Agree | -1.08e+09 1.27e+09 -0.86 0.396 -3.63e+09 1.46e+09 Disag | 1.10e+09 7.85e+08 1.40 0.167 -4.73e+08 2.67e+09 Str disag | 7.90e+08 7.93e+08 1.00 0.324 -7.99e+08 2.38e+09 | country | B | -1.10e+09 5.72e+09 -0.19 0.848 -1.26e+10 1.04e+10 C | -2.02e+09 1.82e+09 -1.11 0.270 -5.67e+09 1.62e+09 D | 2.89e+09 6.28e+09 0.46 0.647 -9.69e+09 1.55e+10 E | 2.07e+09 7.97e+09 0.26 0.797 -1.39e+10 1.80e+10 F | 4.79e+09 3.40e+09 1.41 0.164 -2.02e+09 1.16e+10 G | 0 (omitted) | _cons | -1.26e+09 2.10e+09 -0.60 0.552 -5.48e+09 2.96e+09 ------------------------------------------------------------------------------安慰剂检验
先看第一种方法:改变事件发生时间。该方法假设政策干预时间提前,重新判断政策虚拟变量的系数是否显著。如果不显著,则可以说明原政策效果的稳健性。
以下代码中,假设政策发生事件变为1992年:
gen period = (year>=1992) & !missing(year) // 1994->1992 gen treat = (country>4) & !missing(country) gen did = period * treat reg y period treat did x1-x3 i.opinion i.country, r
β \beta β值变为0.107 F = 0.0025 R-squared = 0.3464 Root MSE = 2.7e+09 ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- period | 2.21e+09 9.84e+08 2.25 0.029 2.40e+08 4.18e+09 treat | 7.49e+08 2.79e+09 0.27 0.789 -4.84e+09 6.33e+09 did | -2.06e+09 1.25e+09 -1.64 0.107 -4.57e+09 4.58e+08 x1 | 1.59e+09 9.57e+08 1.66 0.102 -3.27e+08 3.51e+09 x2 | 7.80e+08 2.80e+09 0.28 0.781 -4.82e+09 6.38e+09 x3 | 1.48e+08 2.83e+08 0.52 0.604 -4.20e+08 7.16e+08 | opinion | Agree | -9.49e+08 1.30e+09 -0.73 0.468 -3.55e+09 1.66e+09 Disag | 9.84e+08 7.85e+08 1.25 0.215 -5.89e+08 2.56e+09 Str disag | 7.90e+08 7.91e+08 1.00 0.322 -7.95e+08 2.38e+09 | country | B | -2.98e+09 6.55e+09 -0.45 0.651 -1.61e+10 1.02e+10 C | -6.99e+08 1.95e+09 -0.36 0.721 -4.60e+09 3.21e+09 D | 5.84e+08 7.13e+09 0.08 0.935 -1.37e+10 1.49e+10 E | -1.69e+09 9.19e+09 -0.18 0.855 -2.01e+10 1.67e+10 F | 2.92e+09 3.59e+09 0.81 0.421 -4.29e+09 1.01e+10 G | 0 (omitted) | _cons | -7.66e+08 2.48e+09 -0.31 0.759 -5.73e+09 4.20e+09 ------------------------------------------------------------------------------
但如果我们仅将政策发生时间提前一年:
gen period = (year>=1993) & !missing(year) // 1994->1993 gen treat = (country>4) & !missing(country) gen did = period * treat reg y period treat did x1-x3 i.opinion i.country, r
结果为: β = 0.015 \beta=0.015 β=0.015,政策效果依然显著。此种情况下,不再能证明原政策效果的稳健性。出现该现状的原因可能是时间提前过少,导致1993年的效果被1994-1999的效果掩盖了。为了避免该尴尬局面的出现,更推荐使用即将介绍的第二种方法:随机化实验组。
Linear regression Number of obs = 70 F(14, 55) = 3.47 Prob > F = 0.0005 R-squared = 0.3826 Root MSE = 2.7e+09 ------------------------------------------------------------------------------ | Robust y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- period | 2.57e+09 8.35e+08 3.08 0.003 9.00e+08 4.25e+09 treat | 1.18e+09 2.67e+09 0.44 0.662 -4.18e+09 6.54e+09 did | -2.94e+09 1.17e+09 -2.52 0.015 -5.27e+09 -6.00e+08 x1 | 1.60e+09 9.21e+08 1.73 0.088 -2.48e+08 3.44e+09 x2 | 9.67e+08 2.67e+09 0.36 0.719 -4.38e+09 6.32e+09 x3 | 1.92e+08 2.91e+08 0.66 0.511 -3.91e+08 7.76e+08 | opinion | Agree | -6.80e+08 1.33e+09 -0.51 0.612 -3.35e+09 1.99e+09 Disag | 9.45e+08 7.39e+08 1.28 0.206 -5.35e+08 2.43e+09 Str disag | 6.35e+08 7.55e+08 0.84 0.404 -8.77e+08 2.15e+09 | country | B | -3.44e+09 6.24e+09 -0.55 0.583 -1.59e+10 9.06e+09 C | -7.09e+08 1.83e+09 -0.39 0.700 -4.38e+09 2.96e+09 D | 1.14e+08 6.71e+09 0.02 0.987 -1.33e+10 1.36e+10 E | -2.18e+09 8.76e+09 -0.25 0.804 -1.97e+10 1.54e+10 F | 2.77e+09 3.40e+09 0.81 0.419 -4.05e+09 9.59e+09 G | 0 (omitted) | _cons | -6.54e+08 2.25e+09 -0.29 0.772 -5.16e+09 3.85e+09 ------------------------------------------------------------------------------在随机化实验组的方法中,一般是随机选取个体作为处理组,重复500次或者1000次,看看“伪政策虚拟变量”的系数是否显著。如果不显著,可以说明原政策效果的稳健性。
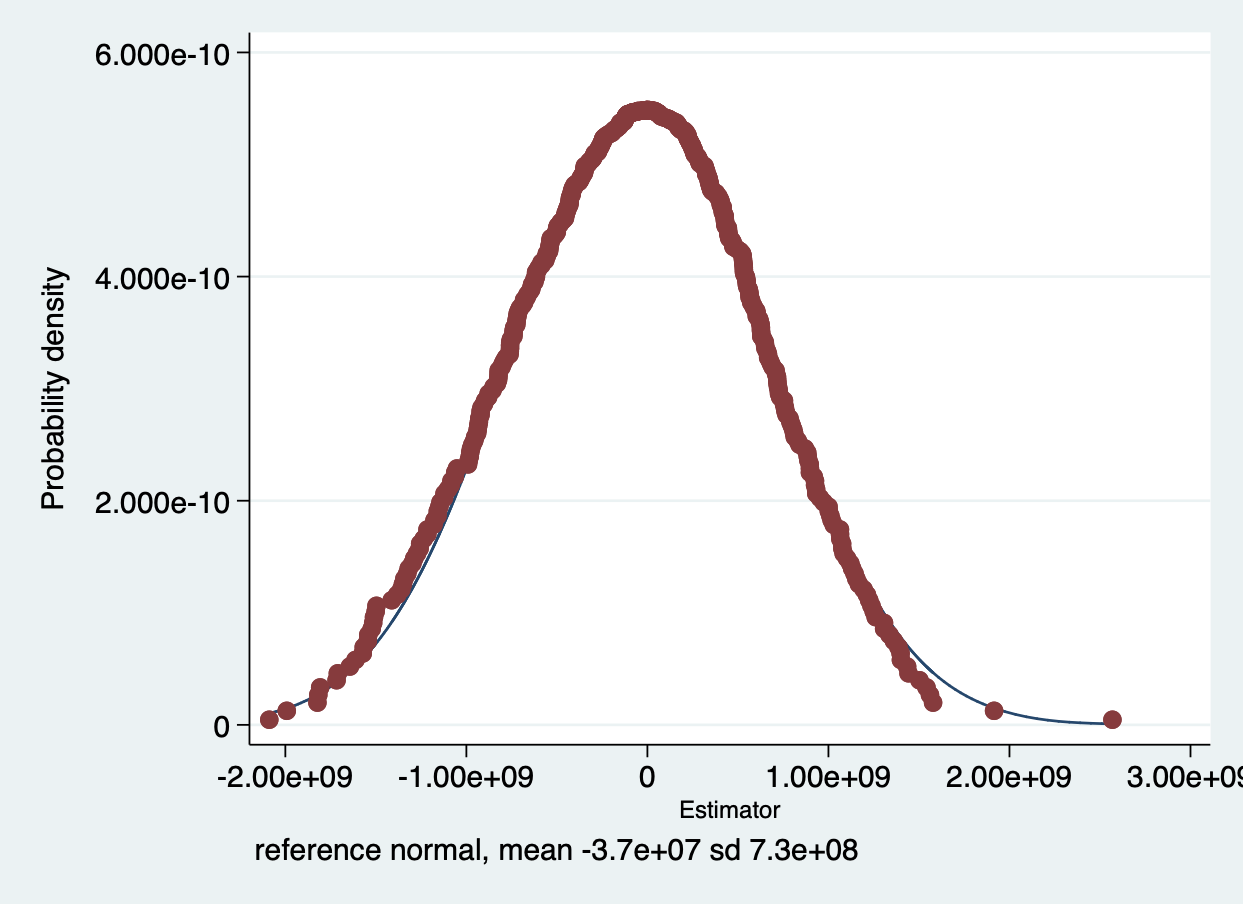
以下是实现代码,因为我自己也不太理解每一步的逻辑,只需要知道该代码能把图绘制出来即可,哈哈~
cap erase "simulations.dta" permute did beta = _b[did] se = _se[did] df = e(df_r), reps(500) seed(2) /// saving("simulations.dta"):reg y did, vce(robust) use "simulations.dta", clear gen t_value = beta / se gen p_value = 2 * ttail(df, abs(beta/se)) dpplot beta, xtitle("Estimator", size(*0.8)) xlabel(, format(%4.3f) labsize(small)) ytitle("Density", size(*0.8)) ylabel(, nogrid format(%4.3f) labsize(small)) note("") caption("") graphregion(fcolor(white))以下是 β \beta β的统计图。从图上可以看出, β \beta β值大部分都都在0附近,平均值为 − 3.7 × 1 0 7 -3.7\times10^7 −3.7×107。回顾效果评估模块中的 β \beta β计算结果,为 1 0 9 10^9 109量级,即随机化的实验组相比原实验组, β \beta β降低了2个数量级,政策效果不再显著。