PyTorch深度学习-06逻辑斯蒂回归（快速入门）

目录

• 1.Logistic Tutorial (逻辑斯蒂回归)
• • 1.1 Why use Logistic (为什么用逻辑斯蒂回归)
  • 1.2 Regression VS Classification (比较回归与分类)
  • 1.3 How to map:R->[0,1] (怎样将实数集映射到区间 [0,1])
  • 2.Sigmoid functions (其他Sigmoid函数)
  • 3.Logistic Regression Model (逻辑斯蒂回归模型)
  • 4.Loss function for Binary Classification (二分类的损失函数)
  • 5.Implementation of Logistic Regression (线性单元和Logistic单元代码比较)
  • 6.总结-完整代码
  • 7.结果截图

    ---

    1.Logistic Tutorial (逻辑斯蒂回归)

    虽然叫回归，但用处是分类

    1.1 Why use Logistic (为什么用逻辑斯蒂回归)

    

    • 从上图中可以看出，此手写数据集一共有10个分类，即y属于{0，1，2，3，4，5，6，7，8，9}，分类的目的就是要估算y属于 0到9的哪一类。
    • 当用线性回归模型做分类问题时，如果输入的是第0个类别，就要让y的输出值为0，如果输入的是第1个类别，就要让y的输出值为1，以此类推。
    • 然而，这种思路并不好，因为在0-9这9个分类中，7和8这两个类是挨着的，而7和9这两个类别中间隔着一个类别8，按理来说应该是7和8的输出值更接近，但实际上，从图中画圈的两个数 可以看出，从笔画的相似性上看，应该是7和9更接近。
    • 所以，在分类问题中，不能用线性回归模型去做，因为这些类别中并没有实数空间中数值大小的概念（即不会认为0比9小）。
    • 分类问题的核心是需要根据输入值x，算出y输出为0的概率P(0)、y输出为1的概率P(1)…一直算到y输出为9的概率P(9)。10个概率值相加等于1，通过比较算出的10个概率值的大小，找出最大概率，就可以判断输入值x属于哪一类。

      

      • download：是否从网上下载数据集，若第一次使用，之前未下载过，就标为True。
      • train：是否为训练集

        1.2 Regression VS Classification (比较回归与分类)

        

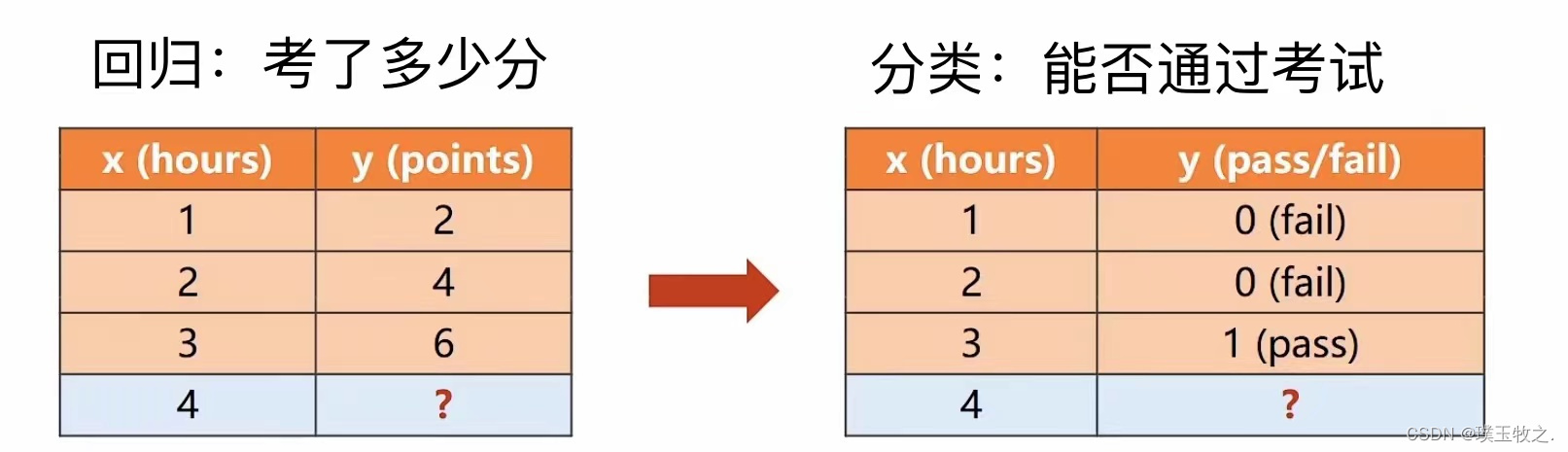
        二分类问题需计算y_hay=1和y_hay=0的概率，但实际上只计算一个值即可。二分类问题只输出1个实数，这个实数表示其中某一个分类的概率，通常y_hat=1的概率为通过考试的概率，若输出值为0.8，就表示通过考试的概率是0.8，判定为通过考试。若输出值范围在0.4-0.6，则会输出不确定。

        1.3 How to map:R->[0,1] (怎样将实数集映射到区间 [0,1])

        

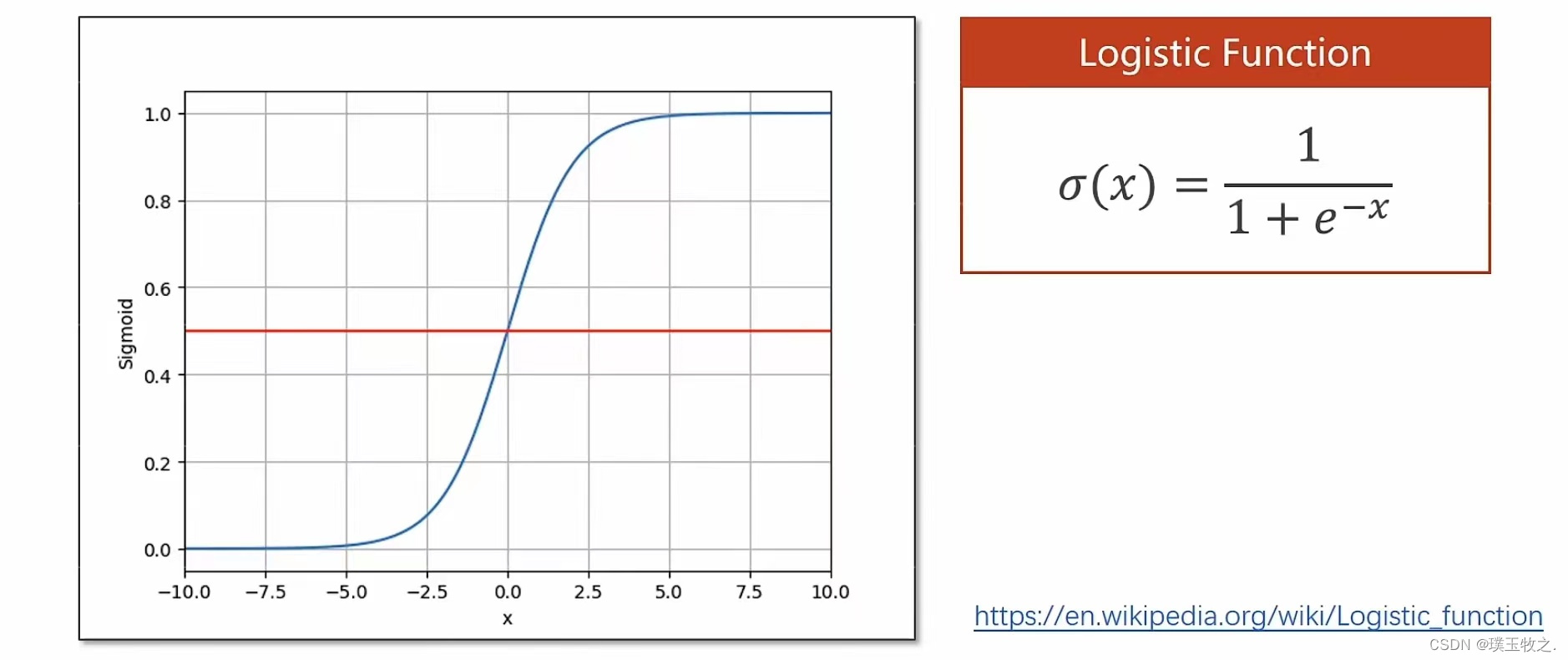
        回归中y_hat的值属于实数集，分类中y_hat的值属于区间 [0,1]，所在分类时，要找到一个函数，把线性模型的输出值由实数空间映射到区间 [0,1]，要找的函数就是Logistic函数

        ps:饱和函数：输入达到一定的值以后，输出就不再变化，达到饱和。Logistic是饱和函数

        

        把线性模型输出的y_hat作为x输入到Logistic函数中，得到的结果就是通过考试的概率。

        2.Sigmoid functions (其他Sigmoid函数)

        

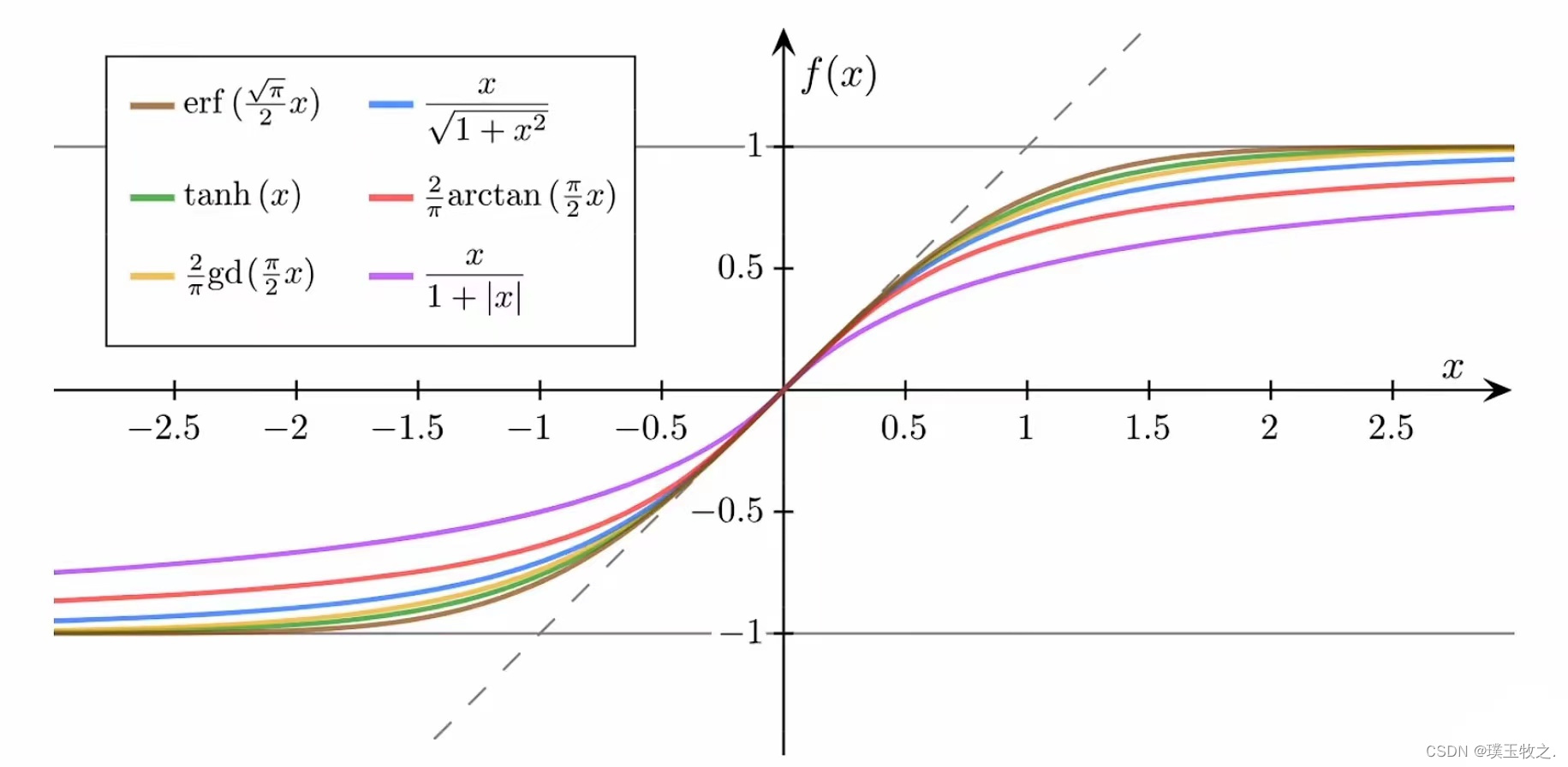
        Sigmoid函数需要满足的条件：

        1. 是饱和函数
        2. 函数值有极限
        3. 是单调增函数

        3.Logistic Regression Model (逻辑斯蒂回归模型)

        

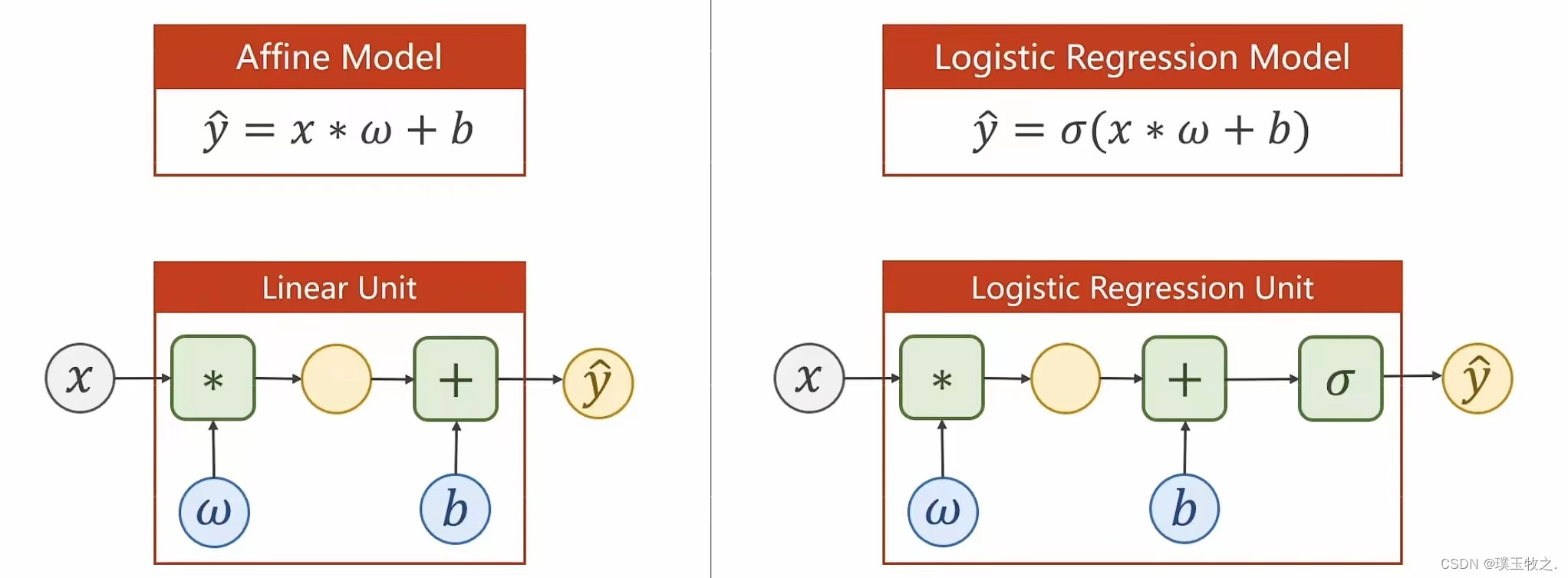
        σ \sigma σ代表Logistic函数

        Logistic函数重要性质：能保证输出值在0 ~ 1之间

        有是希望函数的输出值在-1 ~ 1之间（均值为0），这时就会用到其他Sigmoid函数。

        4.Loss function for Binary Classification (二分类的损失函数)

        Loss function for Binary Classification 简称:：BCE Loss

        

        • Loss Function for Linear Regression是计算数轴上y和y_hat之间的距离，希望loss距离最小化

        • Loss function for Binary Classification输出的是分布，需要比较2个分布之间的差异，希望差异越小越好。y_hat表示分类为1时的概率，1 - y_hat表示分类为0时的概率。若y=0，y = P(class=1) = 0；1 - y = P(class=0) = 1

          

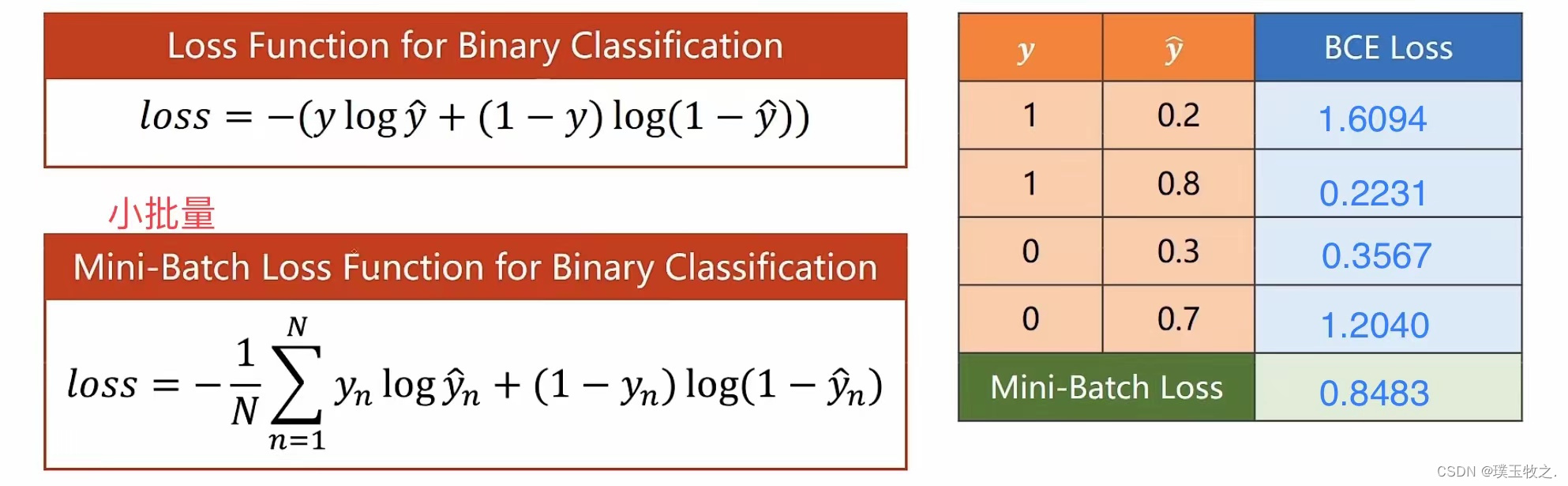
          公式分析：

          5.Implementation of Logistic Regression (线性单元和Logistic单元代码比较)

          

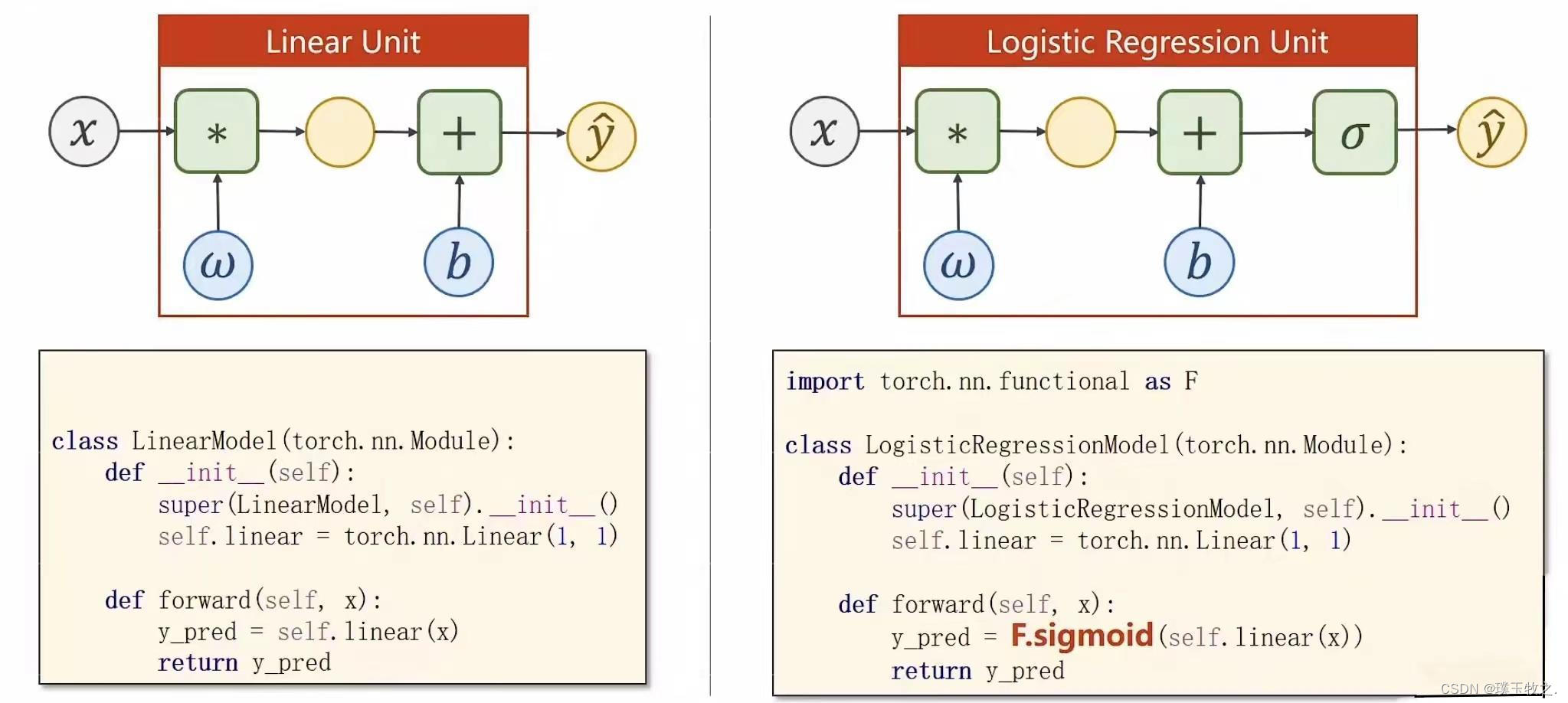
          BCE：交叉熵 (cross-entropy)

          

          6.总结-完整代码

          

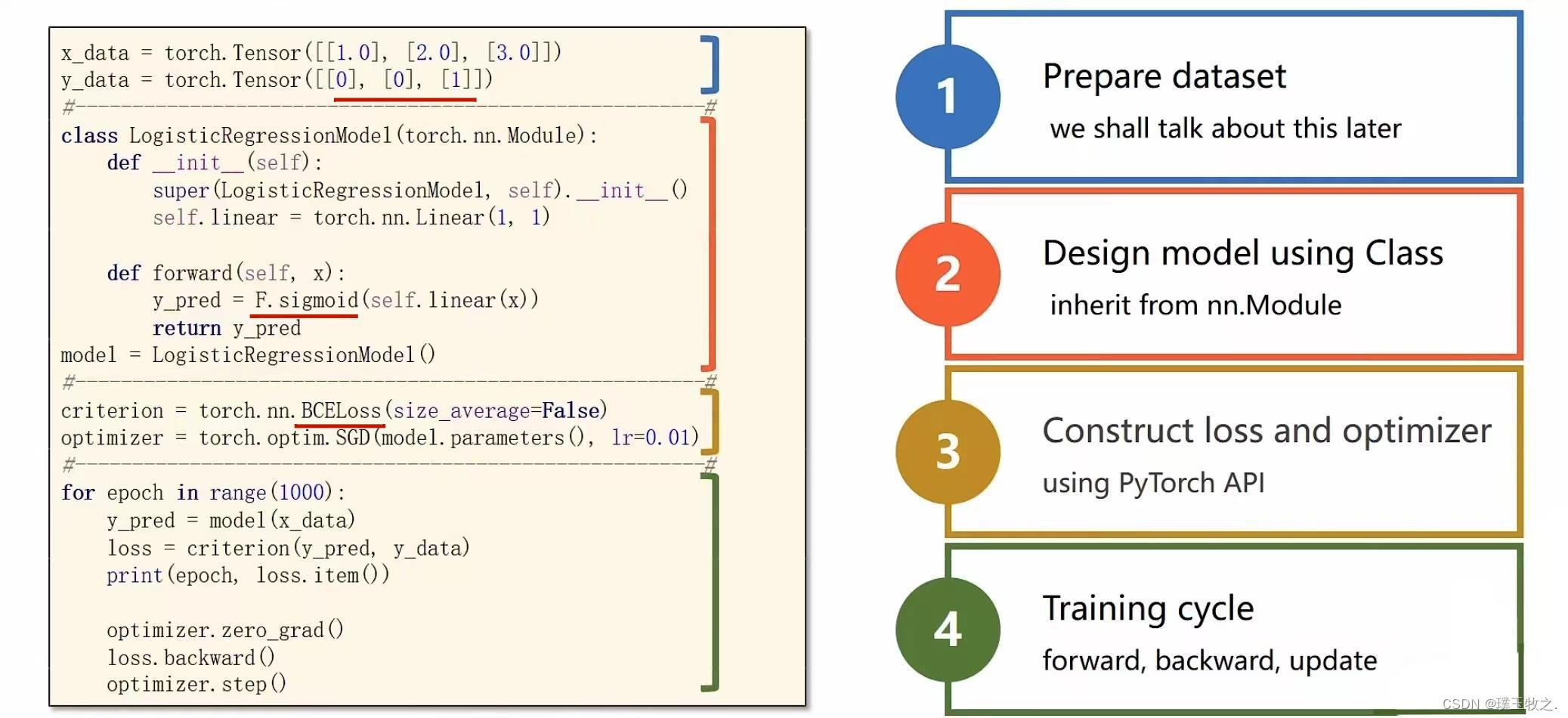
          import numpy as np
          import matplotlib.pyplot as plt
          import torch
          import torch.nn.functional as F
          x_data = torch.Tensor([[1.0], [2.0], [3.0]])
          y_data = torch.Tensor([[0], [0], [1]])
          class LogisticRegressionModel(torch.nn.Module):
              def __init__(self):
                  super(LogisticRegressionModel, self).__init__()
                  self.linear = torch.nn.Linear(1, 1)
              def forward(self, x):
                  y_pred = F.sigmoid(self.linear(x))
                  return y_pred
          model = LogisticRegressionModel()
          criterion = torch.nn.BCELoss(size_average=False)
          optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
          for epoch in range(1000):
              y_pred = model(x_data)
              loss = criterion(y_pred, y_data)
              print(epoch, loss.item())
              optimizer.zero_grad()
              loss.backward()
              optimizer.step()
          x = np.linspace(0, 10, 200)
          x_t = torch.Tensor(x).view((200, 1))
          y_t = model(x_t)
          y = y_t.data.numpy()
          plt.plot(x, y)
          plt.plot([0, 10], [0.5, 0.5], c='r')
          plt.xlabel('Hours')
          plt.ylabel('Probability of Pass')
          plt.grid()
          plt.show()
          

          7.结果截图

          

          

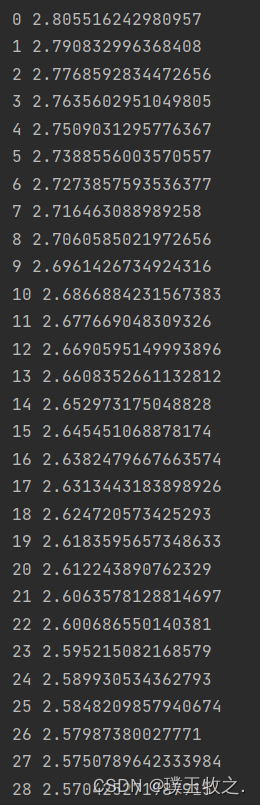
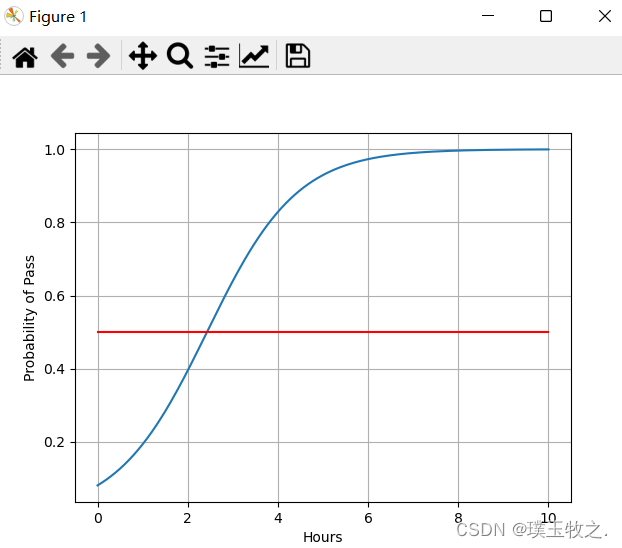
          本文参考：《PyTorch深度学习实践》

          ---

          At the end of my article

          我是璞玉牧之，持续输出优质文章，希望和你一起学习进步！！！原创不易，如果本文对你有帮助，可以 点赞+收藏+评论 支持一下哦！我们下期见~~