遗传算法中的几种不同选择算子及如何用Python实现
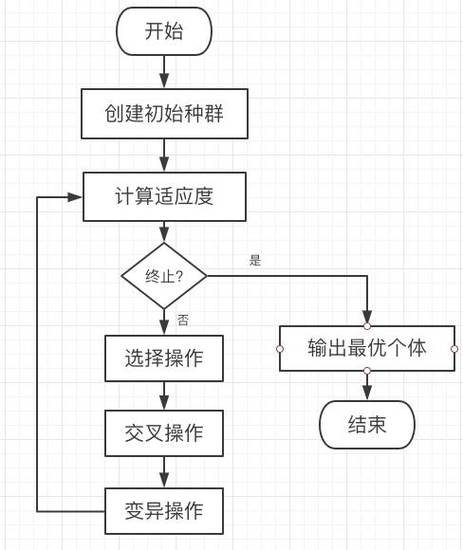
在遗传算法中,选择算子是其中一个关键步骤,它决定了哪些个体将被选中作为下一代的父母,进而影响到后续的进化过程。本文将介绍几种常见的遗传算法选择算子,并提供使用Python实现这些算子的示例代码。
1. 轮盘赌选择(Roulette Wheel Selection):
轮盘赌选择是一种基于概率的选择算子,其思想类似于轮盘赌游戏。每个个体被赋予一个适应度值,适应度值越高,被选中的概率就越大。具体实现时,可以按照适应度值的比例在一个区间内随机选择一个点,然后选择该点所对应的个体作为父母。以下是使用Python实现轮盘赌选择算子的示例代码:
```python
import random
def roulette_wheel_selection(population, fitness_values):
total_fitness = sum(fitness_values)
selection_probs = [fitness / total_fitness for fitness in fitness_values]
cumulative_probs = [sum(selection_probs[:i+1]) for i in range(len(selection_probs))]
parents = []
for _ in range(len(population)):
rand_num = random.random()
for i in range(len(cumulative_probs)):
if rand_num <= cumulative_probs[i]:
parents.append(population[i])
break
return parents
```
2. 锦标赛选择(Tournament Selection):
锦标赛选择是一种竞争性的选择算子,它随机选择一定数量的个体,并从中选出适应度最高的个体作为父母。具体实现时,可以设置一个锦标赛的大小,然后随机选择该大小的个体进行比较,选出其中适应度最高的个体。以下是使用Python实现锦标赛选择算子的示例代码:
def tournament_selection(population, fitness_values, tournament_size):
tournament = random.sample(range(len(population)), tournament_size)
winner_index = max(tournament, key=lambda i: fitness_values[i])
parents.append(population[winner_index])
3. 排序选择(Rank Selection):
排序选择是一种基于适应度排序的选择算子,它将个体按照适应度值的大小进行排序,然后根据排序位置确定被选中的概率。排序选择可以保留适应度较高的个体,并减少适应度较低的个体被选中的概率。以下是使用Python实现排序选择算子的示例代码:
def rank_selection(population, fitness_values):
sorted_indices = sorted(range(len(fitness_values)), key=lambda i: fitness_values[i], reverse=True)
selection_probs = [i / (len(fitness_values) - 1) for i in range(len(fitness_values))]
for i in range(len(selection_probs)):
if rand_num <= selection_probs[i]:
parents.append(population[sorted_indices[i]])
通过以上示例代码,我们可以在遗传算法中使用不同的选择算子来进行个体的选择。这些算子各具特点,可以根据问题的特性和需求选择合适的算子。在实际应用中,我们可以根据问题的复杂程度和计算资源的可用性来选择适当的算子。