如何用C语言将中缀表达式转换为后缀表达式
在计算机科学和数学领域,中缀表达式是最常见的数学表达式表示方法,例如:2 + 3 * 4。然而,对于计算机来说,更容易处理的是后缀表达式(也称为逆波兰表达式),例如:2 3 4 * +。因此,在很多情况下,我们需要将中缀表达式转换为后缀表达式以便进行计算。

下面我们将详细介绍如何使用C语言将中缀表达式转换为后缀表达式:
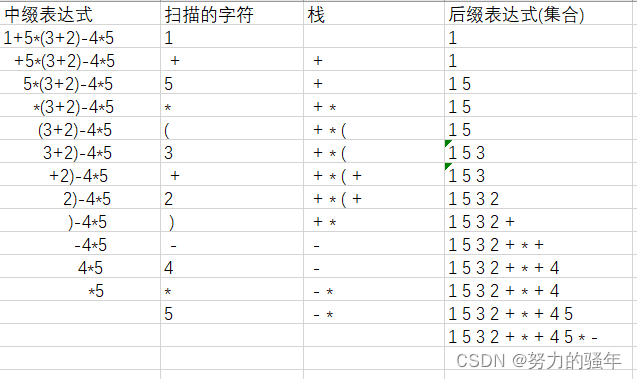
2. 从左到右遍历中缀表达式的每个字符:
- 如果字符是运算符,检查栈顶的运算符:
- 如果栈为空或者栈顶的运算符是左括号"(",则将当前运算符入栈。
- 如果当前运算符的优先级高于栈顶的运算符,则将当前运算符入栈。
- 否则,将栈顶的运算符弹出并添加到输出字符串中,直到满足上述两个条件之一。
- 最后,将当前运算符入栈。
- 如果字符是左括号"(",将其入栈。
- 如果字符是右括号")",则弹出栈顶的运算符并添加到输出字符串中,直到遇到左括号为止。最后,将左括号从栈中弹出。
3. 当中缀表达式遍历完毕后,检查栈是否为空:
- 如果栈不为空,则依次弹出栈顶的运算符并添加到输出字符串中。
4. 输出字符串即为转换后的后缀表达式。
以下是一个使用C语言实现中缀表达式转换为后缀表达式的示例代码:
```c
#include
#include
#include
#define MAX_SIZE 100
// 定义栈结构
typedef struct {
chAR Data[MAX_SIZE];
int top;
} Stack;
// 初始化栈
void initStack(Stack *stack) {
stack->top = -1;
}
// 判断栈是否为空
int isEmpty(Stack *stack) {
return stack->top == -1;
// 入栈
void push(Stack *stack, char c) {
stack->data[++(stack->top)] = c;
// 出栈
char pop(Stack *stack) {
return stack->data[(stack->top)--];
// 获取栈顶元素
char peek(Stack *stack) {
return stack->data[stack->top];
// 判断是否为运算符
int isOperator(char c) {
return (c == '+' || c == '-' || c == '*' || c == '/');
// 获取运算符的优先级
int getPriority(char c) {
if (c == '+' || c == '-')
return 1;
else if (c == '*' || c == '/')
return 2;
else
return 0;
// 将中缀表达式转换为后缀表达式
void infixToPostfix(char *infix, char *postfix) {
Stack stack;
initStack(&stack);
int len = strlen(infix);
int j = 0;
for (int i = 0; i < len; i++) {
char ch = infix[i];
if (isOperator(ch)) {
while (!isEmpty(&stack) && peek(&stack) != '(' && getPriority(peek(&stack)) >= getPriority(ch)) {
postfix[j++] = pop(&stack);
}
push(&stack, ch);
} else if (ch == '(') {
} else if (ch == ')') {
while (!isEmpty(&stack) && peek(&stack) != '(') {
pop(&stack); // 弹出左括号
} else {
postfix[j++] = ch;
}
}
while (!isEmpty(&stack)) {
postfix[j++] = pop(&stack);
postfix[j] = '\0'; // 添加字符串结束符
int main() {
char infix[MAX_SIZE];
char postfix[MAX_SIZE];
printf("请输入中缀表达式:");
gets(infix);
infixToPostfix(infix, postfix);
printf("后缀表达式:%s\n", postfix);
return 0;
```
使用上述代码,你可以输入一个中缀表达式,然后程序将输出对应的后缀表达式。
最后,我们给出一些与该主题相关的标签:C语言、中缀表达式、后缀表达式、栈、逆波兰表达式。