高斯曲线拟合详细步骤、原理及实现
在数据分析和信号处理中,高斯曲线拟合是一种常用的方法,用于估计数据集的概率分布。高斯曲线也被称为正态分布曲线,其形状呈钟形,具有一个峰值和两个对称的尾部。在Matlab中,我们可以使用最小二乘法来拟合高斯曲线,以找到最佳的参数估计。
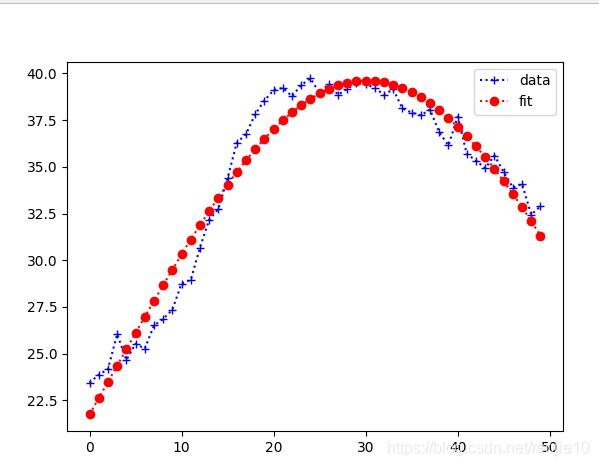
下面将详细介绍高斯曲线拟合的步骤、原理以及如何在Matlab中实现。
步骤:
1. 导入数据:首先,需要导入包含待拟合数据的文件或创建一个数据向量。
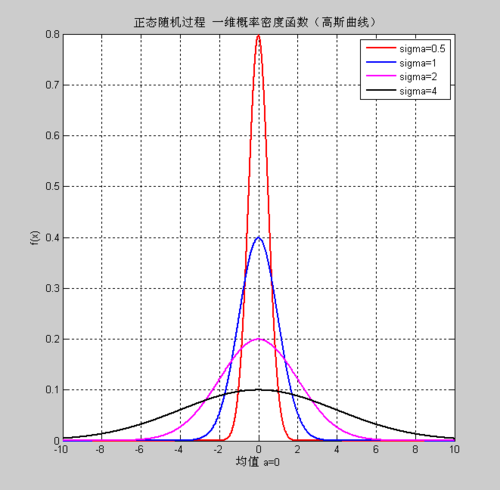
2. 初始化参数:选择适当的初始参数作为高斯曲线的估计值。这些参数通常包括均值、标准差和振幅。
3. 定义高斯函数:使用定义好的高斯函数模型,该模型由均值、标准差和振幅决定。
4. 最小化误差:使用最小二乘法,通过调整参数的值来最小化观测数据与拟合曲线之间的误差。
5. 拟合曲线:根据得到的最佳参数估计值,绘制拟合的高斯曲线。
原理:
高斯曲线是由以下公式定义的:
其中, 是均值, 是标准差。该函数描述了变量在均值附近的概率分布。
最小二乘法用于将观测数据与高斯函数进行拟合。通过调整参数的值,使得观测数据与拟合曲线之间的误差最小化。这可以通过求解误差平方和最小化的优化问题来实现。
Matlab代码实现:
以下是在Matlab中实现高斯曲线拟合的示例代码:
```matlab
% 导入数据
data = load('data.txt');
x = data(:, 1);
y = data(:, 2);
% 初始化参数
mean_init = 0;
std_init = 1;
amplitude_init = 1;
% 定义高斯函数
gaussian = @(x, mean, std, amplitude) amplitude * exp(-(x-mean).^2 / (2*std^2));
% 最小化误差
fit_func = @(params) sum((y - gaussian(x, params(1), params(2), params(3))).^2);
params_fit = fminsearch(fit_func, [mean_init, std_init, amplitude_init]);
% 拟合曲线
x_fit = linspace(min(x), max(x), 1000);
y_fit = gaussian(x_fit, params_fit(1), params_fit(2), params_fit(3));
% 绘制原始数据和拟合曲线
figure;
plot(x, y, 'o', 'MarkerSize', 5);
hold on;
plot(x_fit, y_fit, 'r', 'LineWidth', 2);
xlabel('X');
ylabel('Y');
legend('原始数据', '拟合曲线');
% 输出拟合参数
mean_fit = params_fit(1);
std_fit = params_fit(2);
amplitude_fit = params_fit(3);
disp(['均值: ', num2str(mean_fit)]);
disp(['标准差: ', num2str(std_fit)]);
disp(['振幅: ', num2str(amplitude_fit)]);
```
以上代码首先导入数据,然后定义了高斯函数模型。接下来使用最小二乘法通过调整参数的值来最小化观测数据与拟合曲线之间的误差。最后,绘制原始数据和拟合曲线,并输出拟合得到的参数估计值。