实验二 动态规划
一、实验目的
1、理解动态规划算法的概念;
2、掌握动态规划算法的基本要素;
3、掌握设计动态规划算法的步骤;
4、通过应用范例学习动态规划算法的设计技巧与策略。
二、实验内容和要求
实验要求:通过上机实验进行算法实现,保存和打印出程序的运行结果,并结合程序进行分析,上交实验报告和程序文件。
实验内容:
1、最长公共子序列问题:给定两个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
2、矩阵连乘问题,给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
3、剪绳子问题:给你一根长度为n的绳子,请把绳子剪成m段(m,n都是整数,n>1且m>1),每段绳子的长度记为k[0],k[1],…,k[m-1],请问k[0]×k[1]×…×k[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
三、算法思想分析
1. 动态规划
(1)算法总体思想
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
与分治法不同的是,适合用动态规划法求解的问题,经分解得到的子问题往往不是独立的,存在大量的公共子问题。因此,用动态规划算法求解问题时,我们可依据其递归式以自底向上的方式进行计算。在计算过程中保存已解决的子问题答案。每个子问题只计算一次,在后面计算需要时直接调用,从而避免大量重复计算。
(2)动态规划基本步骤
① 找出最优解的性质,并刻画其结构特征。
② 递归地定义最优值。
③ 以自底向上的方式计算出最优值。
④ 根据计算最优值时得到的信息,构造最优解。
前三个步骤是动态规划算法的基本步骤。在只需求出最优值的情况,步骤四可以省去。若需要求最优解,则必须执行步骤四,根据所记录的信息,快速构造出最优解。
2. 实验内容一分析
(1)问题形式化定义

(2)问题结构分析

(3)递归关系建立
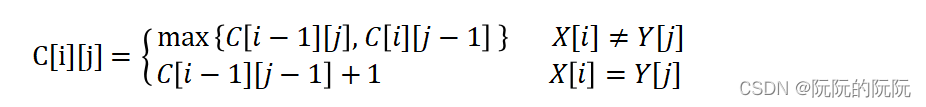
(4)自底向上计算
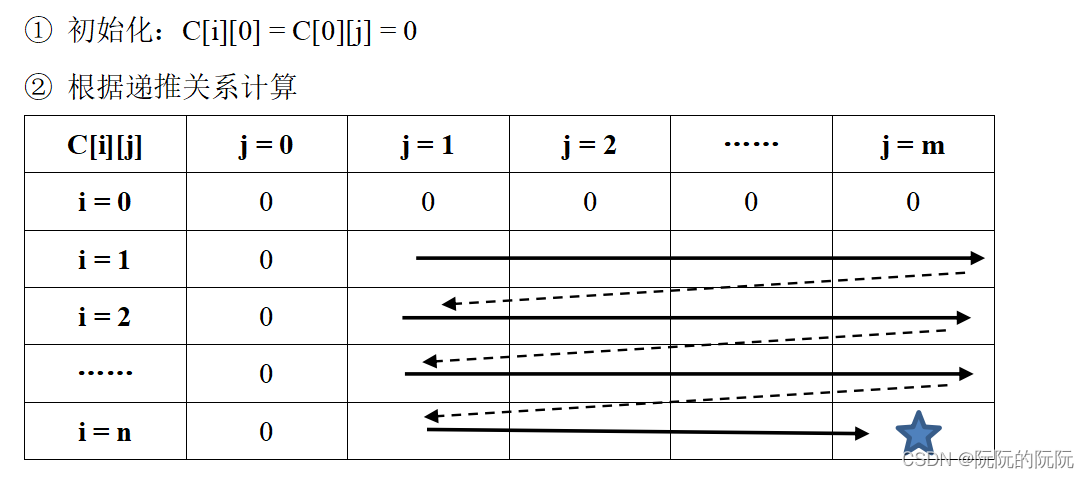
(5)最优方案追踪

3. 实验内容二分析
(1)问题定义
输入:矩阵个数n、矩阵链每个矩阵的行数和最后一个矩阵的列数p[n+1]
输出:找到一种加括号的方式,以确定矩阵链乘法的计算顺序,使得最小化矩阵链标量乘法的次数
(2)问题结构分析

(3)递推关系建立
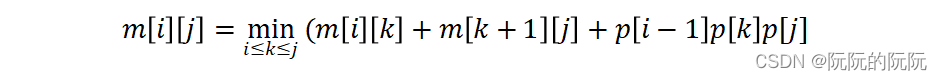
(4)自底向上计算
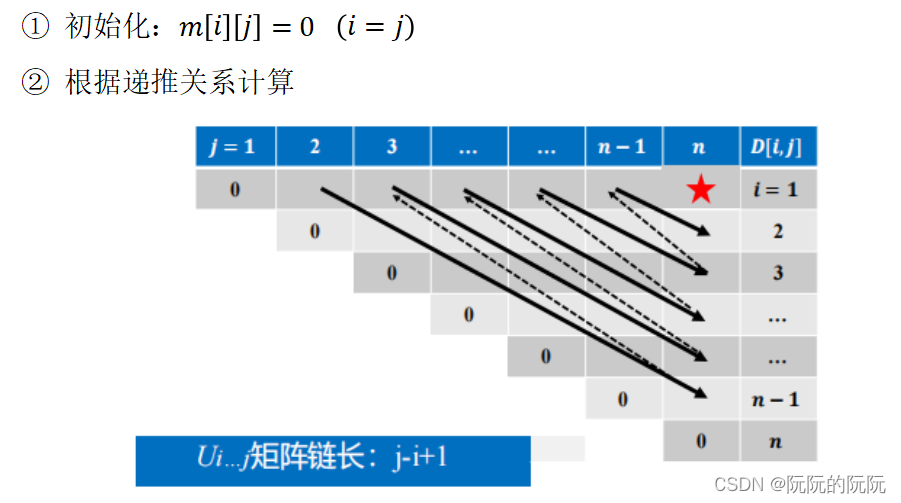
(5)最优方案追踪

4. 实验内容三分析
(1)问题定义
输入:绳长n、欲切成的段数m
输出:找到一种切割方法,使得最大化所有段相乘结果
(2)问题结构分析
① 给出问题表示
a[i][j]:计算长度为i,段数为j的绳子的最大乘积值
② 明确原始问题
a[n][m]:计算长度为n,段数为m的绳子的最大乘积值
(3)递推关系建立
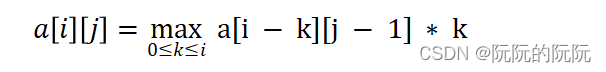
(4)自底向上计算
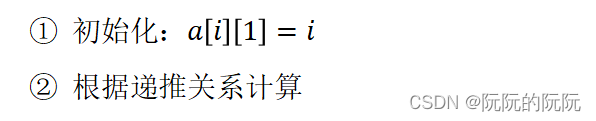
(5)最优方案追踪

四、程序代码
1. 实验内容一
package com.company;
import java.util.Scanner;
public class theMaxChildString {
public static int[][] rec = new int[9999][9999]; //决策数组
public static int theMaxChildString (String text1,String text2) {
// 如果为null或为空字符串,返回
if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) {
return 0;
}
// 转换为字符数组
char[] charString1 = text1.toCharArray();
char[] charString2 = text2.toCharArray();
// 得到数组长度
int len1 = charString1.length;
int len2 = charString2.length;
//最长公共子序列长度计算数组
int[][] dp = new int[len1+1][len2+1];
for (int i = 1;i