时间序列相似度度量
Temporal Sequences Similarity Measurement
Dynamic Time Warping(DTW)
CSDN
CSDN
动态时间归整
-
Key Idea
-
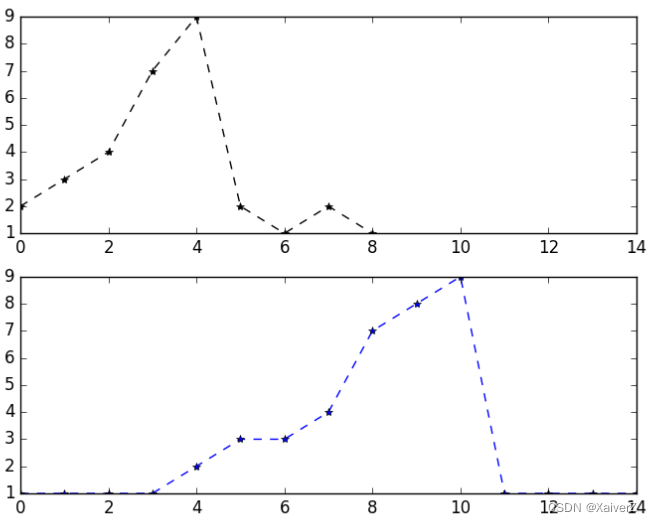
两段时间序列可能存在一定的时间轴方向飘移,在这种情况下,若在同一坐标系下使用欧氏距离衡量两段序列对应逐点距离,则不能很好地反应两段时间序列的相似度
-
在大多数情况下,两个序列整体上具有非常相似的情况,但这些情况在时间轴上并不是对齐的。所以在比较它们之间相似度之前,需要将其中一个或两个序列在时间轴下扭曲(Warping)以达到对齐
-
DTW通过把时间序列进行延伸和缩短,来计算两个时间序列之间的相似性
-
Algorithm
-
现有两个时间序列 Q Q Q与 C C C,一段长为 m m m,一段长为 n n n,每个序列中的元素可以看作是序列的特征向量
-
若 n = m n=m n=m,直接逐点计算序列距离即可
-
若 n ≠ m n \neq m n=m,为了对齐序列,构造一个 n × m n×m n×m的矩阵,其元素 ( i , j ) (i,j) (i,j)表示 q i q_i qi与 c j c_j cj两个点之间的距离(一般为欧氏距离),距离越小相似度越高。DTW的目的就是寻找一条通过此网格中若干格点的路径,路径通过的格点即为两个序列进行序列对齐的点。这条最佳路径称为规整路径(Warping Path)
W = w 1 , w 2 , … , w k , … , w k W=w_{1}, w_{2}, \ldots, w_{\mathrm{k}}, \ldots, w_{\mathrm{k}} W=w1,w2,…,wk,…,wk
max ( m , n ) ≤ K
-
-