【算法系列篇】递归、搜索和回溯（三）

文章目录

• 前言
• 什么是二叉树剪枝
• 1. 二叉树剪枝
• • 1.1 题目要求
  • 1.2 做题思路
  • 1.3 代码实现
  • 2. 验证二叉搜索树
  • • 2.1 题目要求
    • 2.2 做题思路
    • 2.3 代码实现
    • 3. 二叉搜索树中第k小的元素
    • • 3.1 题目要求
      • 3.2 做题思路
      • 3.3 代码实现
      • 4. 二叉树的所有路径
      • • 4.1 题目要求
        • 4.2 做题思路
        • 4.3 代码实现

          前言

          前面我已经给大家分享了两篇关于递归、搜索和回溯相关的问题，但是前面两篇只涉及到了递归，搜索和回溯基本还没涉及到，大家先别着急，后面的文章会为大家分享关于搜索和回溯相关的知识和题目。今天这篇文章主要涉及到的就是关于在递归过程中的剪枝问题。

          什么是二叉树剪枝

          二叉树剪枝是指通过剪去二叉树中某些子树来提高其质量的过程。具体来说，二叉树剪枝可以包括以下几种情况：

          1. 剪去二叉树中所有空子树：当二叉树中存在空子树时，这些空子树不会对整个二叉树的性能产生任何影响，因此可以将它们全部剪去。
          2. 剪去二叉树中重复的子树：当二叉树中存在重复的子树时，这些重复的子树会对整个二叉树的性能产生负面影响，因此可以将它们全部剪去。
          3. 剪去二叉树中不必要的子树：当二叉树中存在一些不必要的子树时，这些子树不会对整个二叉树的性能产生任何影响，因此可以将它们全部剪去。

          通过二叉树剪枝，可以提高二叉树的性能和效率，使得它更加适合于解决实际问题。

          其实二叉树剪枝不困难，只需要我们在递归的过程中做出适当的判断就可以到达剪枝的目的。

          1. 二叉树剪枝

          https://leetcode.cn/problems/binary-tree-pruning/

          1.1 题目要求

          给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

          返回移除了所有不包含 1 的子树的原二叉树。

          节点 node 的子树为 node 本身加上所有 node 的后代。

          示例 1：

          

          输入：root = [1,null,0,0,1]
          输出：[1,null,0,null,1]
          解释：
          只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。
          

          示例 2：

          

          输入：root = [1,0,1,0,0,0,1]
          输出：[1,null,1,null,1]
          

          示例 3：

          

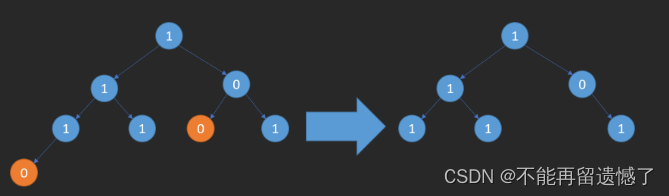
          输入：root = [1,1,0,1,1,0,1,0]
          输出：[1,1,0,1,1,null,1]
          

          提示：

          树中节点的数目在范围 [1, 200] 内
          Node.val 为 0 或 1
          

          /**
           * Definition for a binary tree node.
           * public class TreeNode {
           *     int val;
           *     TreeNode left;
           *     TreeNode right;
           *     TreeNode() {}
           *     TreeNode(int val) { this.val = val; }
           *     TreeNode(int val, TreeNode left, TreeNode right) {
           *         this.val = val;
           *         this.left = left;
           *         this.right = right;
           *     }
           * }
           */
          class Solution {
              public TreeNode pruneTree(TreeNode root) {
              }
          }
          

          1.2 做题思路

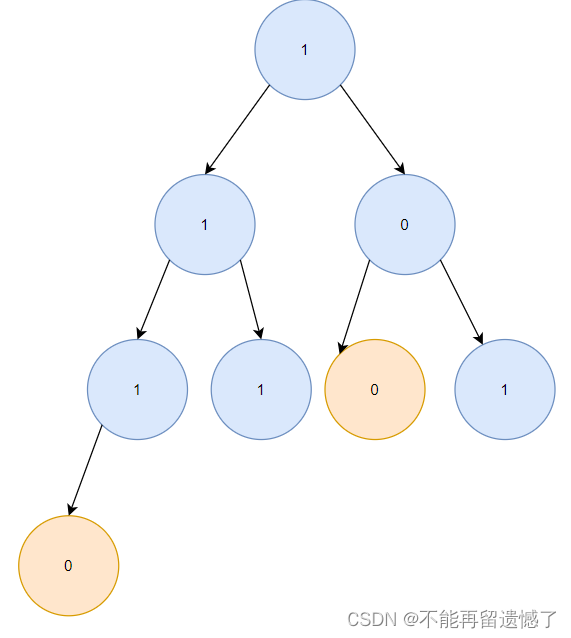
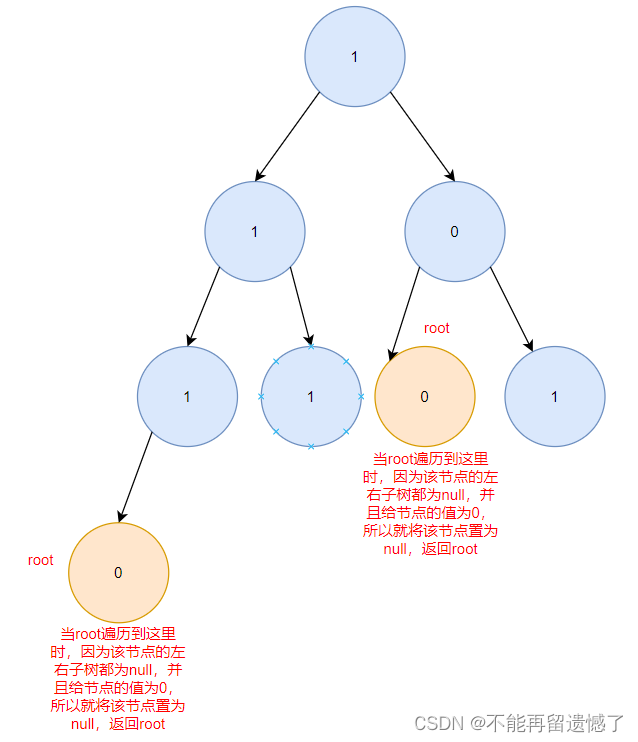
          想要做好递归，我们需要以宏观的视角来解决微观问题。首先先来判断给我们的节点是否是null，如果是则直接返回null，不是，则将根节点的左子树和右子树分别交给函数，通过这个函数，我们不需要知道这个函数的具体细节，我们只需要相信他一定能够帮助我们完成剪枝操作。当根节点的左右子树都完成剪枝操作之后，就进行判断，如果根节点的左右子树都为null，并且根节点的值为0，那么就可以将根节点置为null，然后返回root。

          

          

          1.3 代码实现

          /**
           * Definition for a binary tree node.
           * public class TreeNode {
           *     int val;
           *     TreeNode left;
           *     TreeNode right;
           *     TreeNode() {}
           *     TreeNode(int val) { this.val = val; }
           *     TreeNode(int val, TreeNode left, TreeNode right) {
           *         this.val = val;
           *         this.left = left;
           *         this.right = right;
           *     }
           * }
           */
          class Solution {
              public TreeNode pruneTree(TreeNode root) {
                  if (root == null) return null;
                  root.left = pruneTree(root.left);
                  root.right = pruneTree(root.right);
                  if (root.left == null && root.right == null) {
                      if (root.val == 0) root = null;
                  }
                  return root;
              }
          }
          

          

          2. 验证二叉搜索树

          https://leetcode.cn/problems/validate-binary-search-tree/

          2.1 题目要求

          给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

          有效 二叉搜索树定义如下：

          节点的左子树只包含 小于 当前节点的数。

          节点的右子树只包含 大于 当前节点的数。

          所有左子树和右子树自身必须也是二叉搜索树。

          示例 1：

          

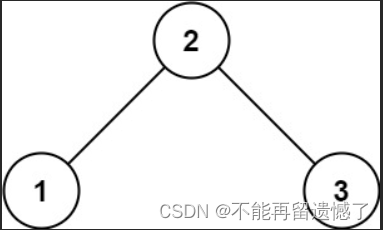
          输入：root = [2,1,3]
          输出：true
          

          示例 2：

          

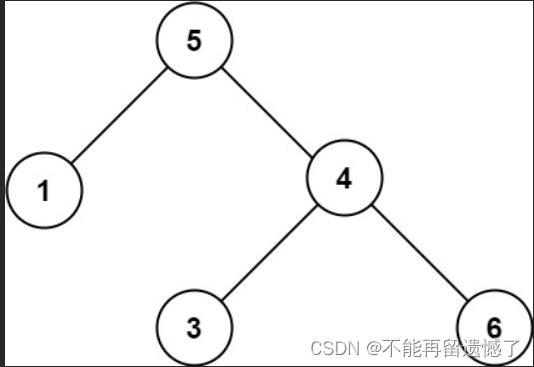
          输入：root = [5,1,4,null,null,3,6]
          输出：false
          解释：根节点的值是 5 ，但是右子节点的值是 4 。
          

          提示：

          树中节点数目范围在[1, 104] 内
          -231 
              public boolean isValidBST(TreeNode root) {
              }
          }
          
              long prev = Long.MIN_VALUE;
              public boolean isValidBST(TreeNode root) {
                  if (root == null) return true;
                  boolean l = isValidBST(root.left);
                  if (l == false) return false;
                  if (root.val  prev) prev = root.val;
                  else return false;
                  boolean r = isValidBST(root.right);
                  return l && r;
              }
          }
          
              public int kthSmallest(TreeNode root, int k) {
              }
          }
          
              int count, ret;
              public int kthSmallest(TreeNode root, int k) {
                  count = k;
                  dfs(root);
                  return ret;
              }
              private void dfs(TreeNode root) {
                  if (count == 0 || root == null) return;
                  dfs(root.left);
                  count--;
                  if (count == 0) {
                      ret = root.val;
                      return;
                  }
                  dfs(root.right);
              }
          }
          
              public List
              }
          }
          
          	//全局的集合变量用来存储二叉树所有路径上的值
              List
                  list = new ArrayList
                  if (root == null) return;
                  //因为StringBuilder的变化不会因为函数的返回而恢复，所以这里我们创建一个临时的StringBuidler类
                  StringBuilder sb = new StringBuilder(s);
                  sb.append(root.val);
                  if (root.left == null && root.right == null) {
                      list.add(sb.toString());
                      return;
                  }
                  //如果当前节点不是叶子节点，那么就加上-
                  sb.append("-");
                  dfs(root.left, sb);
                  dfs(root.right, sb);
              }
          }