分治算法概述
快速排序
练习1:排序数组
练习2:数组中的第K个最大元素
练习3:最小k个数
归并排序
练习4:排序数组
练习5:交易逆序对的总数
练习6:计算右侧小于当前元素的个数
练习7:翻转对
分治算法概述
分治:即 分而治之。也就是将一个大的问题拆分为若干个小问题,然后递归解决每个小问题,最终合并每个小问题的解得到原问题的解
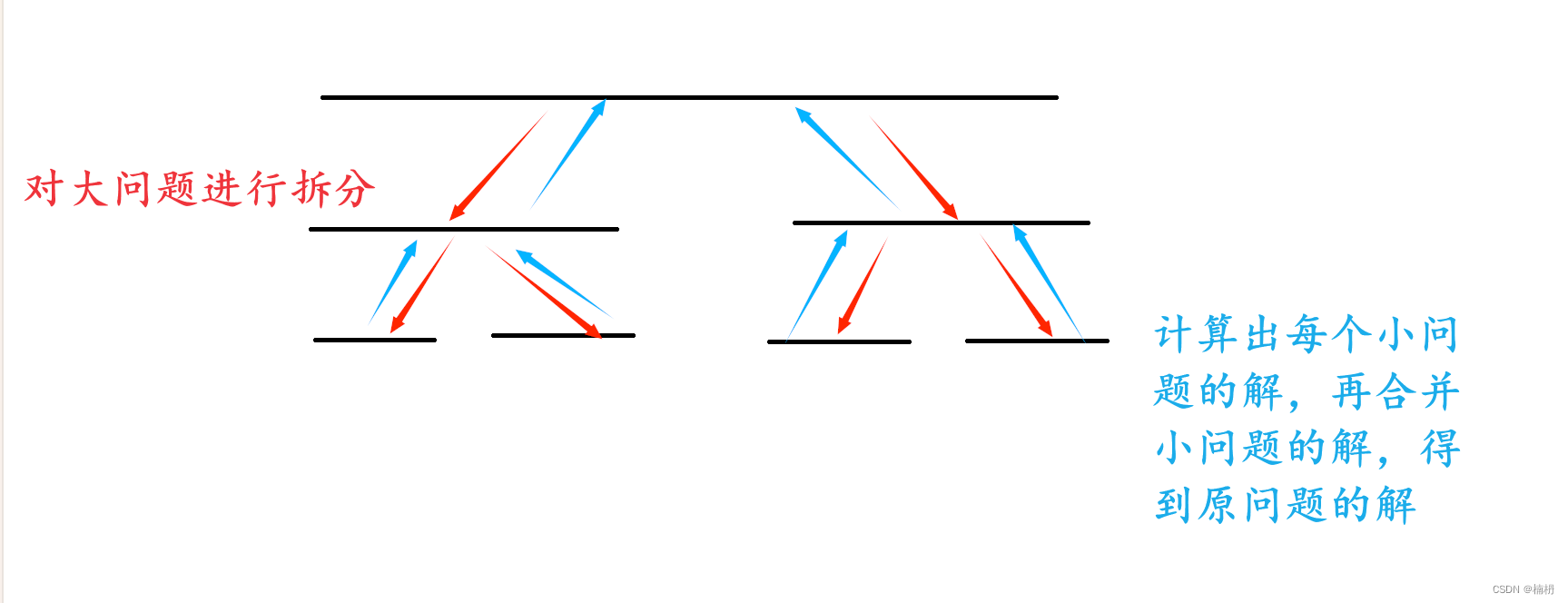
分治算法一般包含 三步:
1. 分割问题:将原问题分割为若干子问题,这些子问题应该是相互独立的,并且和原问题具有相同的结构。
2. 解决子问题:递归解决每个子问题,当子问题足够小时,直接求解
3. 合并子问题的解:将子问题的解合并成原问题的解。
分治的思想体现在 快速排序、归并、二分查找等 中,在本篇文章中,我们重点讲解其在 快速排序和 归并 中的使用。
快速排序
快速排序:用于对数组进行排序,其基本思想是选择一个基准元素,通过将数组中的其他元素按照 与基准元素的大小关系 分为两个(或三个)子数组,然后递归地对这两个(或三个)子数组进行排序,最终将整个数组排序完成。
在分割数组时,可以将数组中的其他元素按照与基准元素的大小关系分为两个子数组,一个子数组中的元素都小于基准元素,另一个子数组中的元素都大于等于基准元素。也可以分为三个子数组,其中,一个子数组中的元素都小于基准元素,一个子数组中的元素都等于基准元素,一个子数组中的元素都大于基准元素。

当将数组分为三块时,等于key区间内的元素已经有序,因此,只需递归排序左边部分和右边部分。当数据中有很多重复数据时,排序效率会大大提升
接下来,我们以一些练习来进一步掌握快速排序
练习1:排序数组
题目链接:
912. 排序数组 - 力扣(LeetCode)
题目描述:
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
- 1








