算法刷题day14

目录

• 引言
• 一、平均
• 二、三国游戏
• 三、松散子序列

  引言

  今天做了三道新题，类型是贪心、枚举、DP，不是特别难，但是努力一下刚好能够够得上，还是不错的，只要能够一直坚持下去，不断刷题不断总结，就是记忆力和毅力了，加油！

  
  （图片来源网络，侵删）

  ---

  一、平均

  标签：贪心

  思路：贪心这种题目只能是见过类似的，然后去变种，一般比赛中是不太可能去现推出来的，这里只讲一下解题思路。这个变数只有四种情况，多变多、多变少、少变多、少变少。

  
  （图片来源网络，侵删）

  1.多变多：多的给多的，那么一个变少了一个变多了，变多了的肯定又要变成少的，所以相当于第一步就多余了，反而代价多了

  2.少变多：少的变多的，那么肯定会有一个多的变成少的，那么就要多变，相当于第一步也就多余了

  3.少变少：其中的一个少的变少了，肯定会有一个多的变成这个少的，所以第一步也多余了

  所以说只能是多的变少的，由于n的数量刚好，所以多余的部分肯定是会变的，要求又得是代价最少，那么就把多余的代价少的那部分变了就行了。

  题目描述：

  有一个长度为 n 的数组（n 是 10 的倍数），每个数 ai都是区间 [0,9] 中的整数。
  小明发现数组里每种数出现的次数不太平均，而更改第 i 个数的代价为 bi，他想更改若干个数的值使得这 10 种数出现的次数相等
  （都等于 n10)，请问代价和最少为多少。
  输入格式
  输入的第一行包含一个正整数 n。
  接下来 n 行，第 i 行包含两个整数 ai,bi，用一个空格分隔。
  输出格式
  输出一行包含一个正整数表示答案。
  数据范围
  对于 20% 的评测用例，n≤1000；
  对于所有评测用例，n≤105，0
      ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
      
      cin > n;
      for(int i = 0; i > a >> b;
          arr[a].push_back(b);
      }
      
      LL res = 0, ave = n / 10;
      for(int i = 0; i  ave)
          {
              sort(arr[i].begin(), arr[i].end());
              for(int j = 0; j yi​+zi​,i∈(1,n)当中任选多个，即 
       
        
         
          
          
            x 
           
          
            i 
           
          
         
           − 
          
          
          
            y 
           
          
            i 
           
          
         
           − 
          
          
          
            z 
           
          
            i 
           
          
         
           > 
          
         
           0 
          
         
           , 
          
         
           i 
          
         
           ∈ 
          
         
           ( 
          
         
           1 
          
         
           , 
          
         
           n 
          
         
           ) 
          
         
           当中任选多个 
          
         
        
          x_i-y_i-z_i>0,i\in(1,n)当中任选多个 
         
        
      xi​−yi​−zi​>0,i∈(1,n)当中任选多个，可以规定一个 
       
        
         
          
          
            w 
           
          
            i 
           
          
         
        
          w_i 
         
        
      wi​来表示左半边，也就是有多个 
       
        
         
          
          
            w 
           
          
            i 
           
          
         
        
          w_i 
         
        
      wi​问最多能选多少个使得它们的和大于0，我们可以把这些 
       
        
         
          
          
            w 
           
          
            i 
           
          
         
        
          w_i 
         
        
      wi​由大到小排序，然后到了边界条件判断一下就可以了。最后结果从三个国家胜出的最大结果中选最大的就行了。 
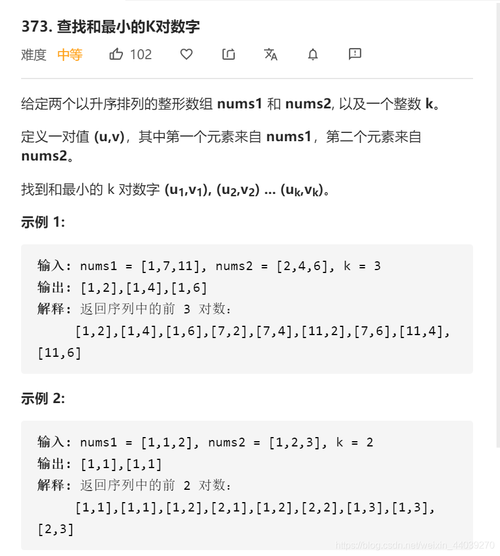
  题目描述：
   
  小蓝正在玩一款游戏。
  游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X,Y,Z（一开始可以认为都为 0）。
  游戏有 n 个可能会发生的事件，每个事件之间相互独立且最多只会发生一次，当第 i 个事件发生时会分别让 X,Y,Z 
  增加 Ai,Bi,Ci。
  当游戏结束时 (所有事件的发生与否已经确定)，如果 X,Y,Z 的其中一个大于另外两个之和，我们认为其获胜。
  例如，当 X>Y+Z 时，我们认为魏国获胜。
  小蓝想知道游戏结束时如果有其中一个国家获胜，最多发生了多少个事件?
  如果不存在任何能让某国获胜的情况，请输出 −1。
  输入格式
  输入的第一行包含一个整数 n。
  第二行包含 n 个整数表示 Ai，相邻整数之间使用一个空格分隔。
  第三行包含 n 个整数表示 Bi，相邻整数之间使用一个空格分隔。
  第四行包含 n 个整数表示 Ci，相邻整数之间使用一个空格分隔。
  输出格式
  输出一行包含一个整数表示答案。
  数据范围
  对于 40% 的评测用例，n≤500；对于 70% 的评测用例，n≤5000；
  对于所有评测用例，1≤n≤105，0≤Ai,Bi,Ci≤109。
  注意，蓝桥杯官方给出的关于 Ai,Bi,Ci 的数据范围是 1≤Ai,Bi,Ci≤109，但是这与给出的输入样例相矛盾，因此予以纠正。
  输入样例：
  3
  1 2 2
  2 3 2
  1 0 7
  输出样例：
  2
  样例解释
  发生两个事件时，有两种不同的情况会出现获胜方。
  发生 1,2 事件时蜀国获胜。
  发生 1,3 事件时吴国获胜。
   
  示例代码：
   
  #include 
  #include 
  #include 
  using namespace std;
  typedef long long LL;
  const int N = 1e5+10;
  int n;
  int a[N], b[N], c[N], w[N];
  LL work(int x[], int y[], int z[])  //x国家胜出
  {
      for(int i = 0; i  0) res = i + 1;
          else break;
      }
      
      return res;
  }
  int main()
  {
      ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
      
      cin >> n;
      for(int i = 0; i > a[i];
      for(int i = 0; i > b[i];
      for(int i = 0; i > c[i];
      
      LL res = max({work(a, b, c), work(b, a, c), work(c, a, b)});
      cout 
      scanf("%s", str+1);
      n = strlen(str+1);
      
      for(int i = 1; i 
          f[i][0] = max(f[i-1][0], f[i-1][1]);
          f[i][1] = f[i-1][0] + str[i] - 'a' + 1;
      }
      
      cout