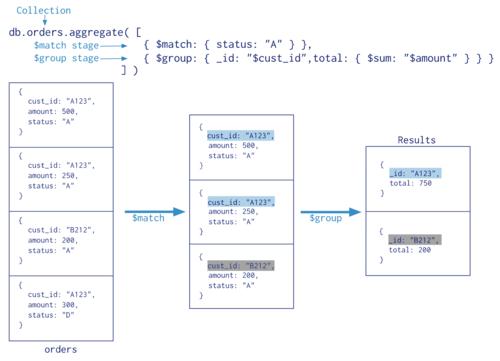
买卖股票相关的动态规划题目
文章目录
- 1.买卖股票的最佳时机含冷冻期
- 2.买卖股票的最佳时期含⼿续费
- 3.买卖股票的最佳时机III
- 4.买卖股票的最佳时机IV
1.最佳买卖股票时机含冷冻期
力扣链接:力扣
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
首先我们分析一下题目,题目中的要点是卖出股票后第二天不能买入,并且每次买新的股票前都要出售掉原先的股票,有了这个限制条件,我们就很容易分析出这道题是多状态的dp。
1.状态表示
当我们以dp[i]表示第i天结束的最大利润时,我们发现无法写出状态转移方程,因为要求第i天的最大利润,我们要看第i天是否是冷冻期或者是否手中无股票或者手中有股票,所以我们将有三种状态表示:
f[i]表示第i天手中有股票的最大利润
g[i]表示第i天手中没有股票的最大利润
s[i]表示第i天处于冷冻期的最大利润
2.状态转移方程

首先我们要分析每种状态,比如我们第i天持有股票,那么从哪一个状态可以到有股票的状态呢?当前一天也就是i-1天就有股票的时候,我们什么也不干到了第i天还是处于有股票的状态。当前一天是没有股票的状态,那么我们在前一天买股票到了第i天就处于有股票状态。
所以f[i] = max(f[i-1],g[i-1] - p[i])
接下来我们分析没有股票的状态,首先如果前一天就没有股票,那么什么也不干到了第i天还是处于没有股票的状态。如果前一天是冷冻期,那么什么也不干到了第i天就自动处于没有股票状态(因为冷冻期一定是卖出股票了,一旦卖出手中就没有股票了)。
所以 g[i] = max(g[i-1],s[i-1])
接下来我们分析冷冻期,冷冻期一定是卖出股票才会有的,所以前一天是有股票状态,然后将股票卖出,第i天就是冷冻期。
所以s[i] = f[i-1] + p[i];
3.初始化
从状态转移方程我们可以看到每次需要前一天的利润,那么只有第1天会越界,所以我们直接初始化三个表的第一天,第一天要有股票那么就得买入,买入利润就从0变成负数,所以f[0] = -p[0]
第一天没有股票那么什么也不干就可以,所以g[0] = 0
第一天就处于冷冻期那么利润一定为0 所以s[0] = 0
4.填表
从左向右,三个表一起填
5.返回值
返回三个表的最后一天的最大值。
class Solution { public: int maxProfit(vector& prices) { int n = prices.size(); vector f(n,0),g(n,0),s(n,0); f[0] = -prices[0]; for (int i = 1;i